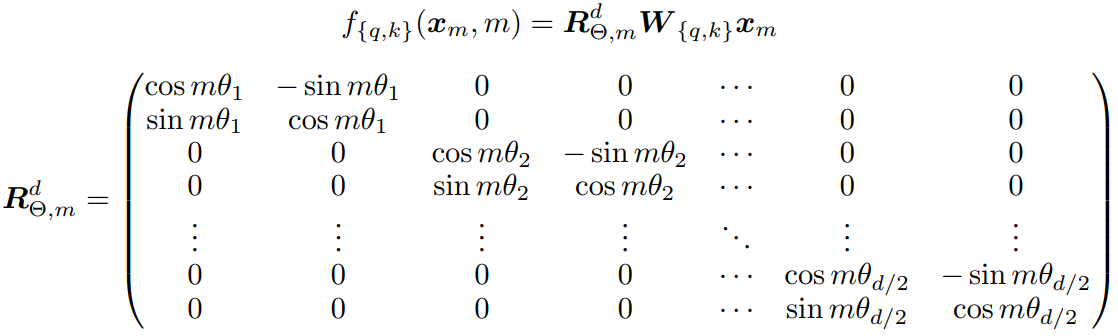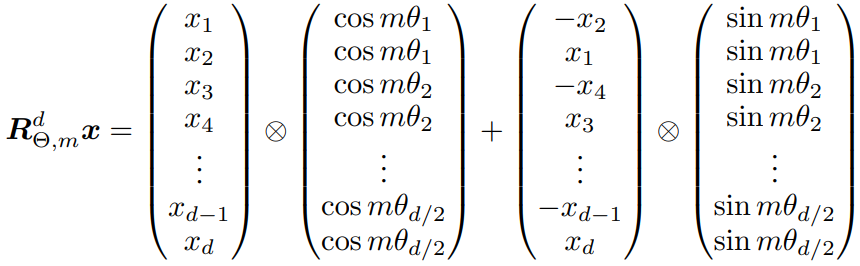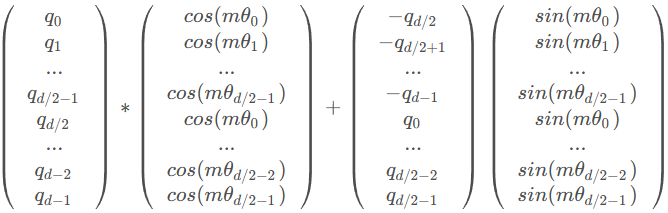huggingface下llama代码细读（上）

huggingface下llama代码细读（上）

llama 是什么

llama 是 meta 公司于 2023 年初发布的一个大语言模型。根据官网上对llama的介绍，meta 公司发布的语言模型可以帮助那些无法拥有大量计算资源的研究人员小成本地进入 AI 大模型领域进行研究。也正因如此，llama 成为了除 ChatGPT 外最有名的大模型之一。为了满足不同级别的研究需要，meta 向全社会提供了经过初步训练的多个不同权重大小的模型数据（7B、13B、33B 和 65B）。

从论文中看，llama 使用了世界上高质量的文本数据进行训练，使用到的训练数据包括：

  • English CommonCrawl [67%]
  • C4 [15%]
  • Github [4.5%]
  • Wikipedia [4.5%]
  • Gutenberg and Books3 [4.5%]
  • ArXiv [2.5%]
  • Stack Exchange [2%]

llama 使用的分词（Tokenizer）算法是由 SentencePiece 实现的 Byte-pair-encoding(BPE) 算法，所有的训练数据大约包含了 1.4T 个 tokens。每个 token 在训练期间仅使用一次，但维基百科和图书等数据除外。在发布 llama 后不久，meta 又发布了 llama-2 模型，接下来，我们会对 llama 和 llama-2 模型架构和实现做详细的讨论。

llama 架构

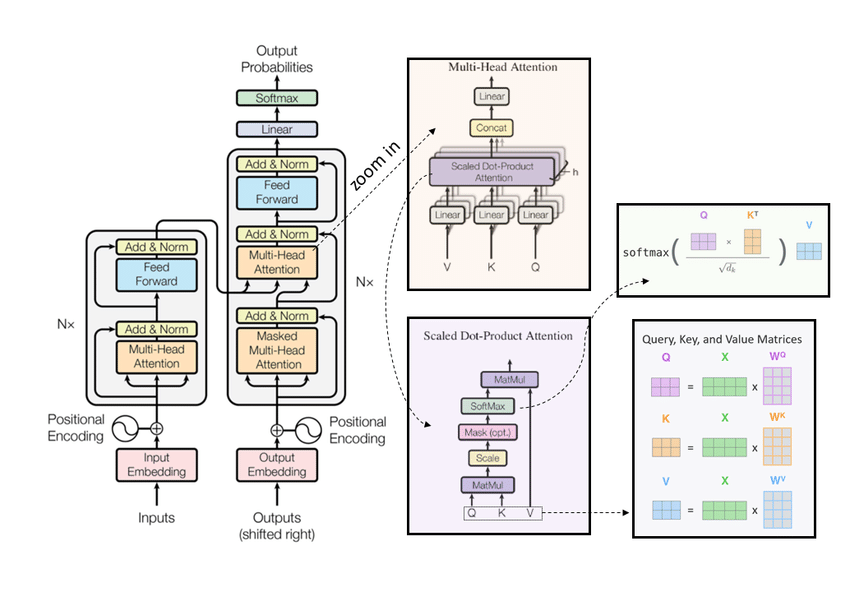
从论文中可知，llama 模型是由大名鼎鼎的 Transformer 架构搭成的，但它也做了如下三点改进：

  • Pre-Normalization Using RMSNorm（使用 RMSNorm 前置归一）
    • What：在 Transformer 架构的基础上，将归一化操作前置到每层的输入前，并改用 Root Mean Square Normalization（RMSNorm）完成归一
    • How：RMS(a)=1n∑inai2RMS(a) = \sqrt{\frac{1}{n}\sum_i^n{a_i^2}}，aˉi=aiRMS(a)gi\bar{a}_i = \frac{a_i}{RMS(a)}g_i；而相比于 Transformer 使用的 layerNorm：μ=1n∑inai\mu = \frac{1}{n}\sum_i^n{a_i}，σ=1n∑in(ai−μ)2\sigma = \sqrt{\frac{1}{n}\sum_i^n{(a_i-\mu)^2}}，aˉi=ai−μσgi\bar{a}_i = \frac{a_i -\mu}{\sigma}g_i
    • Why：为了提升训练的稳定性，对每个 Transformer 子层的输入进行归一化，而不是像原 Transformer 仅对输出进行归一化；此外，相比 layerNorm，RMSNorm 仅支持 re-scaling 计算开销更低，因为研究表明，归一化的主要贡献来自于 re-scaling 而非 re-centering。
  • SwiGLU 激活函数
    • What：非线性处处可导的激活函数，相比原先 Transformer 架构采用的 ReLU 激活函数。
    • How：SwiGLU 其实就是采用 Swish 函数作为激活函数的 GLU 变体，其公式为：SwiGLU(x,W,V,b,c)=Swish1(xW+b)⊗(xV+c)SwiGLU(x, W, V, b, c) = Swish_1(xW+b)\otimes(xV+c)，其中Swishβ(x)=xσ(βx)Swish_\beta(x) = x\sigma(\beta x)
    • Why：该激活函数用科学系的参数，非线性且处处可导，有门控机制可以选择性地过滤部分输入，缓解梯度消失的问题，可以显著提高模型的训练效果。

    GLU（Gated Linear Units）是一种门控机制的神经网络层，它由一个线性变换和一个激活函数组成。例如，若使用 sigmoid 函数作为门控机制，用于控制信息能够通过的“开关”，其公式为GLU(x,W,V,b,c)=σ(xW+b)⊗(xV+c)GLU(x, W, V, b, c) = \sigma(xW+b)\otimes (xV+c)。

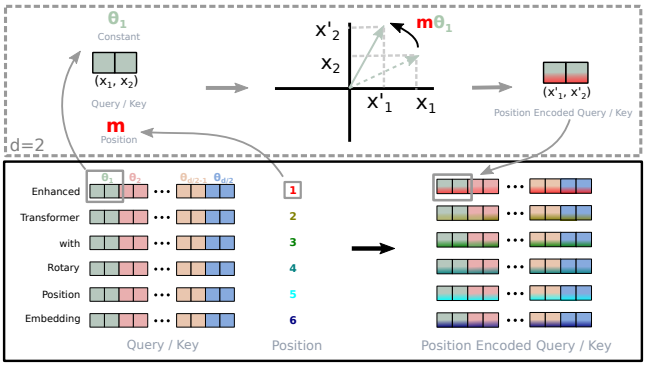
  • Rotaty Embeddings （旋转位置编码 RoPE）
    • What：一种相对位置编码，给输入和输出的文本序列做编号。因为 Transformer 没有保存文本语序的信息，因此需要在输入（输出）时添加位置编码以保证处理的语序结果是正确的
    • How：具体的矩阵编码形式如下图：推理过程参考博采众长的旋转式位置编码。由于从矢量旋转出发推理得到的旋转矩阵过于稀疏（下右图），因此在实际计算时，往往会采用左下图矩阵按位乘的方法并行计算。其中，θi=10000−2(i−1)/d,i∈[1,2,...,d/2]\theta_i = 10000^{-2(i-1)/d}, i \in [1,2,...,d/2]
    • Why：该位置编码有如下特性：上下文表示与旋转矩阵相乘来编码相对位置；可扩展到任意长度，适应任意长度的序列输入输出；可用于线性注意力机制；词间距离与依赖性相关。

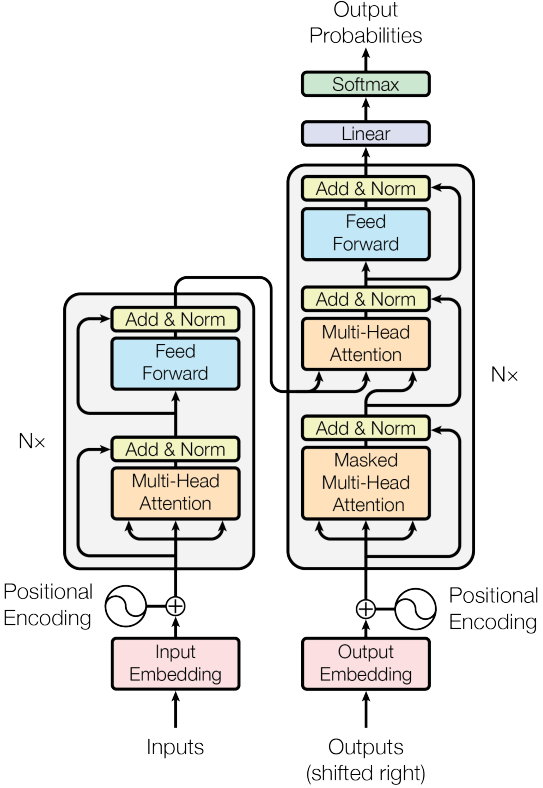
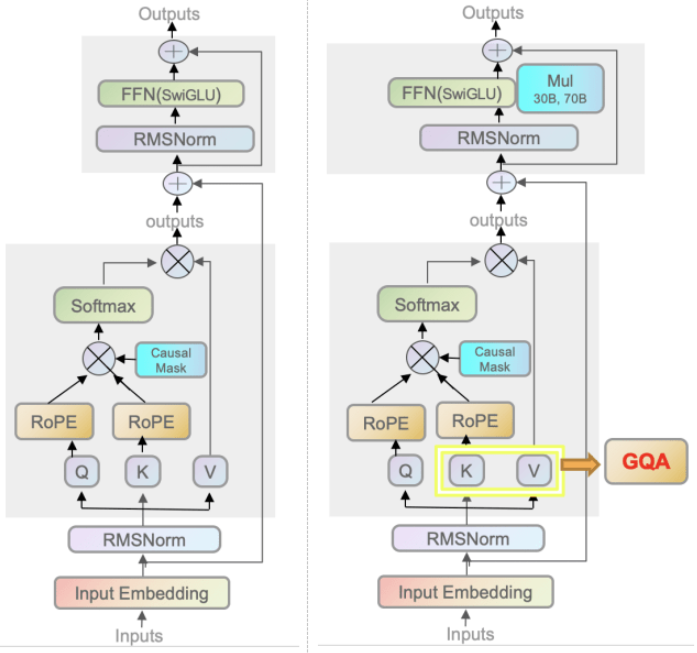
最后，我们来看一下 Transformer、llama、llama-2 模型基块的具体架构图：

llama 基件

随着大语言 AI 模型的不断发展，与之相关的开源社区和开源代码也在不断地丰富和壮大。本博客主要研究 huggingface transformer 开源框架，Huggingface 是一家在 NLP 社区做出杰出贡献的纽约创业公司，其所提供的大量预训练模型和代码等资源被广泛的应用于学术研究当中，现已经发展成为大语言 AI 模型领域中最大的开源社区之一。Huggingface 框架提供了数以千计针对各种任务的预训练模型，开发者可以根据自身的需要，选择模型进行训练或微调，也可参考相关文档和源码，从而快速开发新模型。

本节开始带领大家深入理解 transformers llama 的核心实现。我们先从搭建 llama 的基础组件开始，一步一步从底到顶走过整个代码结构。

RMSNorm

在对 RMSNorm 有一定了解后，我们来看一下 RMSNorm 的实现代码。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class LlamaRMSNorm(nn.Module):
  def __init__(self, hidden_size, eps=1e-6):
    """
    LlamaRMSNorm is equivalent to T5LayerNorm
    """
    super().__init__()
    self.weight = nn.Parameter(torch.ones(hidden_size))
    self.variance_epsilon = eps

  def forward(self, hidden_states):
    input_dtype = hidden_states.dtype
    hidden_states = hidden_states.to(torch.float32)
    variance = hidden_states.pow(2).mean(-1, keepdim=True)
    hidden_states = hidden_states * torch.rsqrt(variance + self.variance_epsilon)
    return self.weight * hidden_states.to(input_dtype)

self.variance_epsilon 是用来规避可能出现的协方差为0的情况而引入的极小值。forward 函数的代码对应了之前给出的公式：RMS(a)=1n∑inai2RMS(a) = \sqrt{\frac{1}{n}\sum_i^n{a_i^2}}以及aˉi=aiRMS(a)gi\bar{a}_i = \frac{a_i}{RMS(a)}g_i。第13、14行将输入的 hidden_states（隐藏状态张量）的最低维度元素，进行平方后取平均，再用 rsqrt 取倒数开根号，最后更新 hidden_states 的值。之后我们会了解到，所谓的最低维度就是张量的特征值 （即 feature 维度）。

激活函数

transformers 的激活函数实现集中在另一个 python 文件中，离我们要讨论的 llama 比较远，实现也较为平凡，不细聊。这里只说明默认使用的是 nn.SiLU 激活函数

RoPE

从上节内容中，我们知道 RoPE 旋转位置编码在推理时的计算过程如上图（这里我们把 x 换成了 transformer 中更常用的 q）。那么关于旋转位置编码的运算，在实际代码中是如何完成的呢？

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class LlamaRotaryEmbedding(nn.Module):
  def __init__(self, dim, max_position_embeddings=2048, base=10000, device=None):
    super().__init__()

    self.dim = dim
    self.max_position_embeddings = max_position_embeddings
    self.base = base
    inv_freq = 1.0 / (self.base ** (torch.arange(0, self.dim, 2).float().to(device) / self.dim))
    self.register_buffer("inv_freq", inv_freq, persistent=False)

    # Build here to make `torch.jit.trace` work.
    self._set_cos_sin_cache(
        seq_len=max_position_embeddings, device=self.inv_freq.device, dtype=torch.get_default_dtype()
    )

首先，LlamaRotaryEmbedding 在构造函数中就将公式中的θi\theta_i存入到 nn.Module 中的 register_buffer。然后调用内部函数将 cos 和 sin 值算出来👇：详细地，torch.einsum 计算了mθim\theta_i，就如论文中配图所示的过程那样（下图，代码中的 t 就是图里的 m），将角度与词的绝对位置相乘，就相当于在平面坐标系上转了一个小角度。最后，将这些值在最低维复制一次，拼接起来（torch.cat），便得到了制备的 cos 和 sin 值。

1
2
3
4
5
6
7
8
9
def _set_cos_sin_cache(self, seq_len, device, dtype):
  self.max_seq_len_cached = seq_len
  t = torch.arange(self.max_seq_len_cached, device=device, dtype=self.inv_freq.dtype)

  freqs = torch.einsum("i,j->ij", t, self.inv_freq)
  # Different from paper, but it uses a different permutation in order to obtain the same calculation
  emb = torch.cat((freqs, freqs), dim=-1)
  self.register_buffer("cos_cached", emb.cos().to(dtype), persistent=False)
  self.register_buffer("sin_cached", emb.sin().to(dtype), persistent=False)

这样做的好处是，所有的 cos 和 sin 值都在程序构造该类时已经计算完成，推理时无需再次计算，加快了推理过程。那么，另一个问题是：在真实的推理中，llama 是如何使用这些已经制备的 cos 和 sin 的？来看下面的代码👇：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
def rotate_half(x):
  """Rotates half the hidden dims of the input."""
  x1 = x[..., : x.shape[-1] // 2]
  x2 = x[..., x.shape[-1] // 2 :]
  return torch.cat((-x2, x1), dim=-1)

def apply_rotary_pos_emb(q, k, cos, sin, position_ids, unsqueeze_dim=1):
  cos = cos[position_ids].unsqueeze(unsqueeze_dim)
  sin = sin[position_ids].unsqueeze(unsqueeze_dim)
  q_embed = (q * cos) + (rotate_half(q) * sin)
  k_embed = (k * cos) + (rotate_half(k) * sin)
  return q_embed, k_embed

# forward for LlamaRotaryEmbedding
def forward(self, x, seq_len=None):
  # x: [bs, num_attention_heads, seq_len, head_size]
  if seq_len > self.max_seq_len_cached:
      self._set_cos_sin_cache(seq_len=seq_len, device=x.device, dtype=x.dtype)

  return (
      self.cos_cached[:seq_len].to(dtype=x.dtype),
      self.sin_cached[:seq_len].to(dtype=x.dtype),
  )

之后会提到，apply_rotary_pos_emb 函数在 LlamaModel:forward 中被调用，计算位置编码。下图公式的第一项和第二项对应代码里的 (q * cos)，注意到 cos 已通过 torch.unsqueeze 列向排布。而公式中的第三项需要靠 rotate_half 获得，方法是切半，旋转，取负，于是得到了下图的运算过程。注意看，虽然论文中描述的公式与下图稍有不同，但其本质仍是一样的。而下图的运算过程能被处理得更加快捷。

RoPE 扩展

llama 中间件

后续内容可能会涉及到 llama 的相关超参。下面的数据是 llama-7b-hf 的 config 数据，后续的内容会对这些参数做具体说明：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
{
  "architecture": ["LlamaForCausalLM"],
  "hidden_act": "silu",
  "hidden_size": 4096,
  "initializer_range": 0.02,
  "intermediate_size": 11008,
  "max_position_embeddings": 4096,
  "model_type": "llama",
  "num_attention_heads": 32,
  "num_hidden_layers": 32,
  "num_key_value_heads": 32,
  "pretraining_tp": 2,
  "rms_norm_eps": 1e-05,
}

MLP

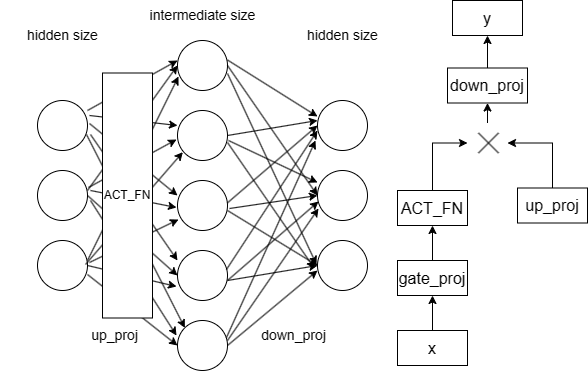
llama 内使用了两层深的 MLP 来存储参数，相对简单。该网络先将维度从 hidden_size 映射到 intermediate_size，再将它降维映射到 hidden_size。具体流程和架构参考下图：

代码中需要注意的是 pretraining_tp 部分，它通过将张量的某一维度简单地均分以实现张量并行（Tensor Parallelism，TP）。例如，第13-17行将线性层的权重矩阵在 intermediate_size 维均分。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class LlamaMLP(nn.Module):
  def __init__(self, config):
    super().__init__()
    self.config = config
    self.hidden_size = config.hidden_size
    self.intermediate_size = config.intermediate_size
    self.gate_proj = nn.Linear(self.hidden_size, self.intermediate_size, bias=False)
    self.up_proj = nn.Linear(self.hidden_size, self.intermediate_size, bias=False)
    self.down_proj = nn.Linear(self.intermediate_size, self.hidden_size, bias=False)
    self.act_fn = ACT2FN[config.hidden_act]

  def forward(self, x):
    if self.config.pretraining_tp > 1:
        slice = self.intermediate_size // self.config.pretraining_tp
        gate_proj_slices = self.gate_proj.weight.split(slice, dim=0)
        up_proj_slices = self.up_proj.weight.split(slice, dim=0)
        down_proj_slices = self.down_proj.weight.split(slice, dim=1)

        gate_proj = torch.cat(
            [F.linear(x, gate_proj_slices[i]) for i in range(self.config.pretraining_tp)], dim=-1
        )
        up_proj = torch.cat([F.linear(x, up_proj_slices[i]) for i in range(self.config.pretraining_tp)], dim=-1)

        intermediate_states = (self.act_fn(gate_proj) * up_proj).split(slice, dim=2)
        down_proj = [
            F.linear(intermediate_states[i], down_proj_slices[i]) for i in range(self.config.pretraining_tp)
        ]
        down_proj = sum(down_proj)
    else:
        down_proj = self.down_proj(self.act_fn(self.gate_proj(x)) * self.up_proj(x))

    return down_proj

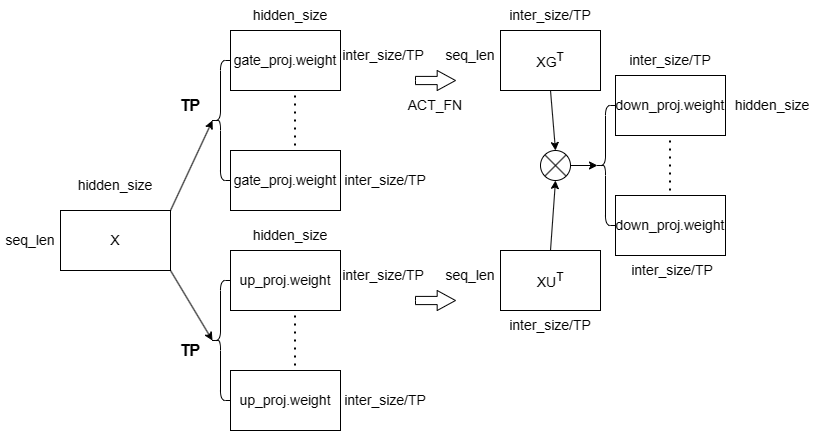
下面这张图展示了 TP 下计算过程，在 intermediate_size 较大时，使用TP对该维度进行均分，可以很好地加速推理过程：MLP 的输入张量 x 在 TP 模式下会在 seq_len 这个维度下被均分成若干子矩阵；每个子矩阵 (seq_len / TP, hidden_size) 都会参与 gate 和 up_proj 的线性层运算，与权重矩阵 (intermediate_size / TP, hidden_size)^T 相乘，得到结果经拼接后，再将分别按位相乘得到中间状态张量 intermediate_states；最后中间状态张量通过 down_proj 线性层得到输出张量。

Attention

注意力机制比较复杂，首先来看一下 LlamaAttention 的构造函数：num_heads 表示注意力头的数量，head_dim 表示注意力头的维度。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class LlamaAttention(nn.Module):
  """Multi-headed attention from 'Attention Is All You Need' paper"""
  def __init__(self, config: LlamaConfig):
    super().__init__()
    self.config = config
    self.hidden_size = config.hidden_size
    self.num_heads = config.num_attention_heads
    self.head_dim = self.hidden_size // self.num_heads
    self.num_key_value_heads = config.num_key_value_heads
    self.num_key_value_groups = self.num_heads // self.num_key_value_heads
    self.max_position_embeddings = config.max_position_embeddings
    self.rope_theta = config.rope_theta
    self.is_causal = True

    if (self.head_dim * self.num_heads) != self.hidden_size:
        raise ValueError(
            f"hidden_size must be divisible by num_heads (got `hidden_size`: {self.hidden_size}"
            f" and `num_heads`: {self.num_heads})."
        )
    self.q_proj = nn.Linear(self.hidden_size, self.num_heads * self.head_dim, bias=config.attention_bias)
    self.k_proj = nn.Linear(self.hidden_size, self.num_key_value_heads * self.head_dim, bias=config.attention_bias)
    self.v_proj = nn.Linear(self.hidden_size, self.num_key_value_heads * self.head_dim, bias=config.attention_bias)
    self.o_proj = nn.Linear(self.num_heads * self.head_dim, self.hidden_size, bias=config.attention_bias)
    self._init_rope()

注意到 q_proj k_proj v_proj o_proj 四个线性层的维度，之后的 TP 会将他们在 hidden_size 拆分，它们的权重张量分别是：

  • q_proj: (num_heads * head_dim, hidden_size)^T
  • k_proj: (num_key_value_heads * head_dim, hidden_size)^T
  • v_proj: (num_key_value_heads * head_dim, hidden_size)^T
  • o_proj: (hidden_size, num_heads * head_dim)^T

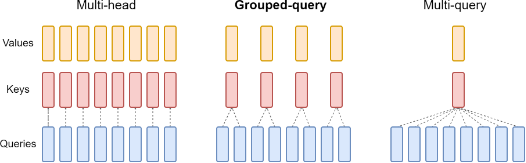
在咱们的 llama-7b-hf 的例子中，注意力头数量较少，因此只有一组注意力头。若注意力头数量较多，llama2 使用分组和 grouped-query attention 机制，使得同一组的 Q 共享一个 KV 权重，减少内存使用，进一步优化推理性能。

forward 实现

forward 函数的实现通常比较复杂，但也有一些简单的小技巧：每次在阅读 forward 函数前，都需要问问自己：正在执行运算的张量维度是什么？张量的维度能很好地帮助我们找到代码中隐藏的蛛丝马迹，更好地读懂这些 python 代码，不迷失在细节之海中。

首先，确认我们的输入张量 hidden_states 的维度：(batch_size, seq_len, hidden_size)。而 QKV 三个权重矩阵的维度也可以从上节线性层初始化中确认，分别是 (num_heads*head_dim, hidden_size)、(num_key_value_heads*head_dim, hidden_size) 和 (num_key_value_heads*head_dim, hidden_size)。在我们的例子中，kv_groups 为1，因此这三个权重矩阵的维度是一样的。

qkv 状态张量

现在来细看一下 咱们是如何切分这些状态张量以实现 TP 的，其实与上文的 MLP 实现极为类似，都是将输入张量的高维均分进行并行计算。第15-17行，query 在最高维度将权重一切为二，18-19 行 key 和 value 也是如此；21-28行，将 hidden_states（就是输入）与 query 权重相乘，TP 并行计算完后在最后一个维度上合并，同理于 key 和 value。忽略最高维的 batch_size，具体运算公式如下：

query=Hseq_len,hidden_sizeQnum_heads∗head_dim,hidden_sizeTquery = H_{seq\_ len, hidden\_size} Q_{num\_heads*head\_dim, hidden\_size}^T 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
def forward(
    self,
    hidden_states: torch.Tensor,
    attention_mask: Optional[torch.Tensor] = None,
    position_ids: Optional[torch.LongTensor] = None,
    past_key_value: Optional[Tuple[torch.Tensor]] = None,
    output_attentions: bool = False,
    use_cache: bool = False,
    **kwargs,
) -> Tuple[torch.Tensor, Optional[torch.Tensor], Optional[Tuple[torch.Tensor]]]:
  bsz, q_len, _ = hidden_states.size()

  if self.config.pretraining_tp > 1:
    key_value_slicing = (self.num_key_value_heads * self.head_dim) // self.config.pretraining_tp
    query_slices = self.q_proj.weight.split(
        (self.num_heads * self.head_dim) // self.config.pretraining_tp, dim=0
    )
    key_slices = self.k_proj.weight.split(key_value_slicing, dim=0)
    value_slices = self.v_proj.weight.split(key_value_slicing, dim=0)

    query_states = [F.linear(hidden_states, query_slices[i]) for i in range(self.config.pretraining_tp)]
    query_states = torch.cat(query_states, dim=-1)

    key_states = [F.linear(hidden_states, key_slices[i]) for i in range(self.config.pretraining_tp)]
    key_states = torch.cat(key_states, dim=-1)

    value_states = [F.linear(hidden_states, value_slices[i]) for i in range(self.config.pretraining_tp)]
    value_states = torch.cat(value_states, dim=-1)

  else:
    query_states = self.q_proj(hidden_states)
    key_states = self.k_proj(hidden_states)
    value_states = self.v_proj(hidden_states)

RoPE 位置编码

准备好 query_states、key_states、value_states 线性层后，紧接着就是将输入张量加上旋转矩阵位置编码。但在一切开始之前，注意到 1-3 行将张量的维度做了很大的变化。以 query_states 为例，原先的维度是 (num_heads*head_dim, hidden_size)，现在将维度 view 后接转置成了 (batch_size, num_heads, seq_len, head_dim)。同理与其他 states，于是下一行的 kv_seq_len 为何取 shape[-2] 就可以理解了。上文提及过，位置编码的余弦值和正弦值计算完成后，apply_rotary_pos_emb 在这里被调用。

1
2
3
4
5
6
7
8
9
# ... to be continued
query_states = query_states.view(bsz, q_len, self.num_heads, self.head_dim).transpose(1, 2)
key_states = key_states.view(bsz, q_len, self.num_key_value_heads, self.head_dim).transpose(1, 2)
value_states = value_states.view(bsz, q_len, self.num_key_value_heads, self.head_dim).transpose(1, 2)

kv_seq_len = key_states.shape[-2]
# ...
cos, sin = self.rotary_emb(value_states, seq_len=kv_seq_len)
query_states, key_states = apply_rotary_pos_emb(query_states, key_states, cos, sin, position_ids)

注意，不同于原先的 transformer 架构，LlamaAttention 在每次前推注意力机制时都会加上位置编码。

Grouped-Query Attention

接着往下看，抛开 past_key_value 的部分，直接跳到第9-10行，注意此时 kv 状态张量的维度是 (batch_size, num_kv_heads, kv_seq_len, head_dim)，而经过 repeat_kv 函数的操作后，kv 状态张量变成了 (batch_size, num_kv_heads*num_kv_groups, kv_seq_len, head_dim)，也就是说，内部的权重被复制了 num_kv_groups 遍。具体过程会在后续列出。而再对比一下 query_states 的维度，这意味着同一组的 query 会共享同一个 kv 权重。这就是 llama2 提出的 Grouped-Query Attention 技术，这可以减少权重的内存开销，而实验表明，这样处理后模型的精度不会差很多。

最后，在第 12 行完成了 torch.matmul 执行 QK 矩阵相乘，得到注意力机制权重。从QK两者的维度我们不难得出，attn_weights 的维度是 (batch_size, num_heads, seq_len, kv_seq_len)。这一步完成了公式QKTdk\frac{QK^T}{\sqrt{d_k}}的计算。

1
2
3
4
5
6
7
8
9
10
11
if past_key_value is not None:
  # reuse k, v, self_attention
  key_states = torch.cat([past_key_value[0], key_states], dim=2)
  value_states = torch.cat([past_key_value[1], value_states], dim=2)

past_key_value = (key_states, value_states) if use_cache else None

key_states = repeat_kv(key_states, self.num_key_value_groups)
value_states = repeat_kv(value_states, self.num_key_value_groups)

attn_weights = torch.matmul(query_states, key_states.transpose(2, 3)) / math.sqrt(self.head_dim)

这里有 repeat_kv 函数实现：

1
2
3
4
5
6
7
8
9
10
def repeat_kv(hidden_states: torch.Tensor, n_rep: int) -> torch.Tensor:
  """
  This is the equivalent of torch.repeat_interleave(x, dim=1, repeats=n_rep). The hidden states go from (batch,
  num_key_value_heads, seqlen, head_dim) to (batch, num_attention_heads, seqlen, head_dim)
  """
  batch, num_key_value_heads, slen, head_dim = hidden_states.shape
  if n_rep == 1:
    return hidden_states
  hidden_states = hidden_states[:, :, None, :, :].expand(batch, num_key_value_heads, n_rep, slen, head_dim)
  return hidden_states.reshape(batch, num_key_value_heads * n_rep, slen, head_dim)

输入的张量在2维度复制了一份，因此所有比2维度低的数据（即 None 后低维度的数据）都复制了 n_rep 遍，最后这些数据会被合并到1维度上。因而最后得到的张量维度是 (batch_size, num_kv_heads*num_kv_groups, seq_len, head_dim)，其中2、3维度的数据被复制了 n_rep 遍。就如同下图所示的那样。

收尾

接着往下看：第7行表示若存在 attention_mask 则需要将其加到权重上，这与 transformer decoder 的行为一致。因为咱们这次仅关注 forward 过程，不涉及训练，在推理生成文本序列时，attention_mask 的作用就是防止 decoder 受到未生成张量的影响。10 行将得到的权重放入 softmax 激活函数，11 行再将注意力权重与 v 状态张量相乘，从而完成了softmax(QKTdk)Vsoftmax(\frac{QK^T}{\sqrt{d_k}})V运算。这就完成了该子层的运算，该子层的输出就是下一层的输入。因此输出张量的维度必然与输入维度一致，所以16行将原先被转置的矩阵重新拨回来，17行又将张量变成了 (batch_size, seq_len, hidden_size)。

最后在 19-22 行，因为上面的计算步骤其实是 TP 的，因此最后还要将结果合并。注意，21行还会经过一个线性层。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
if attention_mask is not None:
  # if attention_mask.size() != (bsz, 1, q_len, kv_seq_len):
  attn_weights = attn_weights + attention_mask

# upcast attention to fp32
attn_weights = nn.functional.softmax(attn_weights, dim=-1, dtype=torch.float32).to(query_states.dtype)
attn_output = torch.matmul(attn_weights, value_states)

if attn_output.size() != (bsz, self.num_heads, q_len, self.head_dim):
  # raise ValueError

attn_output = attn_output.transpose(1, 2).contiguous()
attn_output = attn_output.reshape(bsz, q_len, self.hidden_size)

if self.config.pretraining_tp > 1:
    attn_output = attn_output.split(self.hidden_size // self.config.pretraining_tp, dim=2)
    o_proj_slices = self.o_proj.weight.split(self.hidden_size // self.config.pretraining_tp, dim=1)
    attn_output = sum([F.linear(attn_output[i], o_proj_slices[i]) for i in range(self.config.pretraining_tp)])
else:
    attn_output = self.o_proj(attn_output)

return attn_output, attn_weights, past_key_value

至此，咱们已经分析完 llama 所有的基本组件。让我们再次回到这个架构图，细细回味一下张量在前推过程中经历的所有。

关于 FlashAttention2

小结

本文从 llama 是什么出发，深入解读了 huggingface 框架对 llama 的代码实现。我先从 llama 论文开始解读，试图让所有未接触过大模型的外行人能理解大模型是用什么训练而成的。随后，我介绍了 llama 的架构图，并简要说明了 llama1/2 和 transformer 框架的区别，以及为何要这样改进。本博客重点分析了 llama 的各个基件和中间件，从底至上地分析了 hugginface llama 的实现，由于我也是第一次如此细致地阅读大模型的代码，因此很多地方可能会比较啰嗦。但万事开头难，在研究的最初阶段尽可能搞清楚最基本的东西，步步为营方能豁然开朗。下一篇论文将介绍 llama 每一层的实现与组合，主要是利用本篇博客中介绍的组件搭建起译码层的故事，并借此说明大模型推理的主要流程。当然，我不可能面面俱到地介绍所有细节，但也能揭开大模型的神秘面纱，从中瞥见一些人工智能的奥秘。

AI
#AI #Transformer
huggingface下llama代码细读（上）
https://dingfen.github.io/2023/10/30/2023-10-30-huggingface1/
作者
Bill Ding
发布于
2023年10月30日
更新于
2024年5月19日
许可协议