DeepSeek 背后的 MLA 和 MoE 架构

最近，DeepSeek（深度求索）公司推出的 DeepSeek-V3 和 DeepSeek-R1 大火，吸引了太平洋两岸所有关心关注 AI 发展的人的目光。本文试图从 DeepSeek 这轮爆火现象的背后，探究其中的架构创新，进而挖掘它如此低廉却好用的原因。

MLA(Multi-head Latent Attention)

一句话说明什么是 MLA

为了进一步解决 KV cache 在模型推理中的性能瓶颈，MLA 架构使用了两个低秩矩阵来压缩 KV cache，减轻缓存压力，从而提升了推理性能。

看图说话——MLA是如何工作的

结合 vllm 最新版本（v0.6.6.post1）和 DeepSeek-V3 论文内的符号，我绘制了下面的计算流程图：

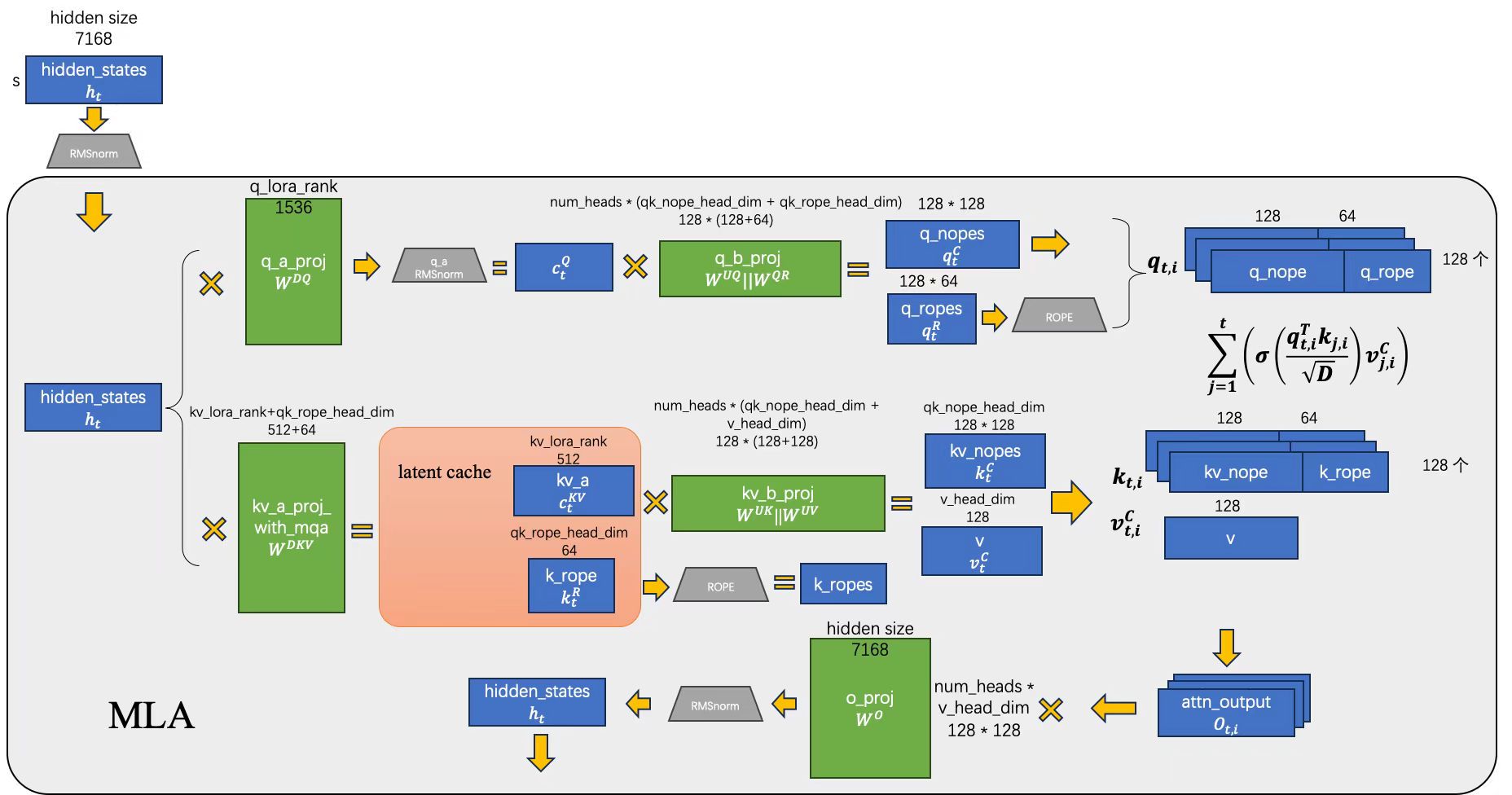
1. 让我们从这副图的左上角开始，首先，input hidden $h_t$ 经过一次 RMSNorm 后，进入到了 MLA 层。
2. $h_t$ 会被分为两条路径，上面一条路径用来产生 $q_{t,i}$，下面的路径产生 $k_{t,i}$ 和 $v_{t,i}$
3. 先来关注上一条路径 $q_{t,i}$，不同于之前传统的 attention 机制：$W^Qh_t$ 来计算出 Query，MLA 使用了两个低秩矩阵来代替 $W^Q$:

$$c^Q_t=W^{DQ}h_t \tag{1}$$

$$\{q^C_t,q^R_t\}=\{W^{UQ}c^Q_t,\operatorname{RoPE}(W^{QR}c^Q_t) \} \tag{2}$$

这两个低秩矩阵就是上面式子中的 $W^{DQ}$ 和 $W^{UQ}$，分别表示是 down proj 和 up proj 的 query 权重矩阵。$W^{QR}$ 是用于产生携带 RoPE 信息的部分 query。这里涉及到 MLA 的另一个创新：不同于传统的 attention 机制，MLA 仅使部分 QKV 携带 RoPE 的位置编码信息。

4. 更重要的 KV cache 这边的下一条路径。同样的思路，使用两个低秩的矩阵 $W^{DKV}$ + $W^{KR}$ 和 $W^{UK}$ + $W^{UV}$ 来计算出 key，方法是首先计算出 latent 张量：

$$c^{KV}_t=W^{DKV}h_t \tag{3}$$

然后使用 $c^{KV}_t$ 来计算 key：

$$\{k^C_t, k^R_t\}=\{W^{UK}c^{KV}_t,\operatorname{RoPE}(W^{KR}h_t)\} \tag{4}$$

同样地，对于 Value 张量：

$$v^C_t=W^{UV}c^{KV}_t \tag{5}$$

$W^{DKV}$，$W^{UK}$ 和 $W^{UV}$ 分别表示 down proj 的 KV 权重矩阵，up proj 的 K V 权重矩阵。$W^{KR}$ 是用于产生携带 RoPE 信息的那一部分 key。同样地，再重复一遍：不同于传统的 attention 机制，MLA 仅有后部分 QKV 携带 RoPE 的位置编码信息。

5. 在图的右半部分，我们将3 4 步得到的 QKV 做 MHA(Multi-Head Attention) ，这里想必大家都挺熟了的:

   $$o_{t,i}=\sum^t_{j=1}{\sigma(\frac{q^T_{t,i}k_{j,i}}{\sqrt{D}})v^C_{j,i}}\tag{6}$$

6. 最后，在图的最下面，我们将 atten 得到的结果再做一次 o proj 和 RMSNorm，得到的 hidden states 就可以传给后续的 MoE/MLP 层了：

   $$u_t=W^O\{o_{t,1};o_{t,2};...;o_{t,n}\} \tag{7}$$

将一个大矩阵替换成两个低秩矩阵，节约了多少权重大小？

我们来计算一下，用此方法的低秩矩阵究竟能节省多少权重？以 DeepSeek-V3 为例，其 hidden size 是 7168，num heads 是 128，head dim 是 192，那么传统的 $W^Q$ 维度是 (7168, 128x192)，而$W^{DQ}$ 维度是 (7168, 1536) 和 $W^{UQ}$ 维度是 (1536, 128x192)，节省了 72.3% 的权重。

同样来计算一下这方法可以节省多少权重？按照图中给出的 DeepSeek-V3 模型的数据规模：若使用传统的 attention，那么 $W^K$ 和 $W^V$ 都是 (7168, 128x192) 大小；而 MLA 中 $W^{DKV}$ 是 (7168, 512)，$W^{KR}$ 是 (7168, 64)，$W^{UK}$ 和 $W^{UV}$ 都是 (512, 128x128) 大小的，因此总共可以节省 94.1%。

将一个大矩阵替换成两个低秩矩阵，如何能降低 KV Cache 容量，节约了多少缓存容量？

答：传统 attn 机制中，要存放到 KV cache 大小有 2 x num kv heads x head dim x sizeof(dtype)。而在 MLP 中，要存放的 KV cache 大小被缩减为了 dim x sizeof(dtype) 大小。

就拿 deepseek-v3 为例，如果使用传统的 attn 机制，那么每个 token 每一层需要占用 2 x 128 x 192 x sizeof(dtype) = 49152 Bytes，而 MLA 下每个 token 每一层仅需要 576 Bytes。节约了将近 98.8% 的 KV cache。

使用两个低秩矩阵是否会导致计算变多变慢？

答：关于矩阵吸收的理解

Update On Oct. 05

---

之前错误理解了矩阵吸收这个概念，现在我们根据代码实现再来梳理一下到底何为矩阵吸收。

我们参考的是 sglang deepseek_v2.py 内的相关代码实现，首先来看一下正常情况（矩阵不吸收）：

def forward_normal_prepare(
     self,
     positions: torch.Tensor,
     hidden_states: torch.Tensor,
     forward_batch: ForwardBatch,
     zero_allocator: BumpAllocator,
 ):
     if self.q_lora_rank is not None:
         # q = LayerNorm(H*q_a_proj)*q_b_proj
         q, latent_cache = self.fused_qkv_a_proj_with_mqa(hidden_states)[0].split(
             [self.q_lora_rank, self.kv_lora_rank + self.qk_rope_head_dim], dim=-1
         )
         q = self.q_a_layernorm(q)
         q = self.q_b_proj(q)[0].view(-1, self.num_local_heads, self.qk_head_dim)
     else:
         # ...
     # latent = LayerNorm(H*kv_a_proj)*kv_b_proj
     _, q_pe = q.split([self.qk_nope_head_dim, self.qk_rope_head_dim], dim=-1)
     kv_a, _ = latent_cache.split([self.kv_lora_rank, self.qk_rope_head_dim], dim=-1)
     latent_cache = latent_cache.unsqueeze(1)
     kv_a = self.kv_a_layernorm(kv_a)
     kv = self.kv_b_proj(kv_a)[0]
     kv = kv.view(-1, self.num_local_heads, self.qk_nope_head_dim + self.v_head_dim)
     k_nope = kv[..., : self.qk_nope_head_dim]
     v = kv[..., self.qk_nope_head_dim :]
     k_pe = latent_cache[:, :, self.kv_lora_rank :]
     q_pe, k_pe = self.rotary_emb(positions, q_pe, k_pe)
     q[..., self.qk_nope_head_dim :] = q_pe
     k = torch.empty_like(q)

     # Temporary for DeepSeek V3/R1 only, but can generalize if needed
     if (
         _is_cuda
         and (self.num_local_heads == 128)
         and (self.qk_nope_head_dim == 128)
         and (self.qk_rope_head_dim == 64)
     ):
         concat_mla_k(k=k, k_nope=k_nope, k_rope=k_pe)
     else:
         k[..., : self.qk_nope_head_dim] = k_nope
         k[..., self.qk_nope_head_dim :] = k_pe

     if not _is_npu:
         latent_cache[:, :, : self.kv_lora_rank] = kv_a.unsqueeze(1)
         latent_cache[:, :, self.kv_lora_rank :] = k_pe

         # Save latent cache
         forward_batch.token_to_kv_pool.set_kv_buffer(
             self.attn_mha, forward_batch.out_cache_loc, latent_cache, None
         )
     else:
         # ...

     return q, k, v, forward_batch

 def forward_normal_core(self, q, k, v, forward_batch):
     attn_output = self.attn_mha(q, k, v, forward_batch, save_kv_cache=False)
     attn_output = attn_output.reshape(-1, self.num_local_heads * self.v_head_dim)
     output, _ = self.o_proj(attn_output)
     return output

仔细研读发现，上面代码的相关矩阵维度是：

Name	Dim
H:	[q_len, H]
Q_a_proj:	[q_len, H] * [H, q_lora_rank]
Q_b_proj:	[q_len, q_lora_rank] * [q_lora_rank, n *(qk_nope_dim + qk_rope_dim)]
得到 Q:	[q_len, n * (qk_nope_dim + qk_rope_dim)]
KV_a_proj_with_mqa:	[q_len, H] * [H, kv_lora_rank + qk_rope_dim]
K_b_proj:	[q_len, kv_lora_rank] * [kv_lora_rank, n * (qk_nope_dim + v_head_dim)]
得到 K:	[q_len, n * (qk_nope_dim + qk_rope_dim)]
AttnCore:	Q * K_t: [n, q_len, (qk_rope_dim + qk_nope_dim)] * [n, (qk_nope_dim + qk_rope_dim), kv_len]
AttnScore * V:	[n, q_len, kv_len] * [n, kv_len, v_head_dim]
OutProj:	[b,s,n/tp v_h] [n/tp * v_h, H]

$${q^C_t}^Tk^C_t=(W^{UQ}c^Q_t)^T(W^{UK}c^{KV}_t)$$

让我们再来看看矩阵吸收的代码，有所删减：

def forward_absorb_prepare(
    self,
    positions: torch.Tensor,
    hidden_states: torch.Tensor,
    forward_batch: ForwardBatch,
    zero_allocator: BumpAllocator,
):
    from sglang.srt.model_executor.cuda_graph_runner import get_is_capture_mode

    if self.q_lora_rank is not None:
        if (
            (not isinstance(hidden_states, tuple))
            and hidden_states.shape[0] <= 16
            and self.use_min_latency_fused_a_gemm
        ):
            # H * qkv_a_proj
            fused_qkv_a_proj_out = dsv3_fused_a_gemm(
                hidden_states, self.fused_qkv_a_proj_with_mqa.weight.T
            )
        else:
            # ...
        q, latent_cache = fused_qkv_a_proj_out.split(
            [self.q_lora_rank, self.kv_lora_rank + self.qk_rope_head_dim], dim=-1
        )
        k_nope = latent_cache[..., : self.kv_lora_rank]

        # overlap qk norm
        if self.alt_stream is not None and get_is_capture_mode():
            current_stream = torch.cuda.current_stream()
            self.alt_stream.wait_stream(current_stream)
            q = self.q_a_layernorm(q)
            with torch.cuda.stream(self.alt_stream):
                k_nope = self.kv_a_layernorm(k_nope)
            current_stream.wait_stream(self.alt_stream)
        else:
            # ...

        k_nope = k_nope.unsqueeze(1)
        q = self.q_b_proj(q)[0].view(-1, self.num_local_heads, self.qk_head_dim)
    else:
        # ...

    q_nope, q_pe = q.split([self.qk_nope_head_dim, self.qk_rope_head_dim], dim=-1)
    k_pe = latent_cache[..., self.kv_lora_rank :].unsqueeze(1)

    if self.use_deep_gemm_bmm:
        # ...
    elif _is_hip:
        # TODO(haishaw): add bmm_fp8 to ROCm
        # ...
    elif self.w_kc.dtype == torch.float8_e4m3fn:
        # ...
    else:
        # q * W_kc
        q_nope_out = torch.bmm(q_nope.transpose(0, 1), self.w_kc)

    q_nope_out = q_nope_out.transpose(0, 1)

    if not self._fuse_rope_for_trtllm_mla(forward_batch) and (
        not _use_aiter or not _is_gfx95_supported
    ):
        q_pe, k_pe = self.rotary_emb(positions, q_pe, k_pe)

    return q_pe, k_pe, q_nope_out, k_nope, forward_batch, zero_allocator, positions

Name	Dim
Q_a_proj:	[q_len, H] * [H, q_lora_rank]
Q_b_proj:	[q_len, q_lora_rank] * [q_lora_rank, n *(qk_nope_dim + qk_rope_dim)]
此时 Q:	[q_len, n * (qk_nope_dim + qk_rope_dim)]
W_uk_from_kv_b_proj：	[n, q_len, qk_nope_dim] * [n, qk_nope_dim, kv_lora_rank]
Q 与 W^UK × 后：	[n, q_len, kv_lora_rank]
KV_a_proj_with_mqa:	[q_len, H] * [H, kv_lora_rank + qk_rope_dim]
得到的 K:	[q_len, kv_lora_rank + qk_rope_dim]
AttnCore:	Q * K_t: [n, q_len, kv_lora_rank + qk_rope_dim] * [kv_lora_rank + qk_rope_dim, kv_len]
AttnScore * V:	[n, q_len, kv_len] * [kv_len, kv_lora_rank]
W_uv_from_kv_b_proj:	[q_len, n, kv_lora]*[n, kv_lora, v_head_dim]
OutProj:	[q_len, n * v_head_dim] * [n * v_head_dim, H]

$${q^C_t}^Tk^C_t=(W^{UQ}c^Q_t)^TW^{UK}c^{KV}_t={c^Q_t}^T{(W^{UQ})}^TW^{UK}c^{KV}_t=({c^Q_t}^T{W^{UQ}}^TW^{UK})c_t^{KV}$$

对比 Attention 输入的 QK 差别，我们可以发现，矩阵吸收时， K/V tensor Shape 中不携带 num_heads 维度数据，即 [q_len, kv_lora_rank + qk_rope_dim]，也就是转换成了 MQA 计算。

正常模式下， K/V tensor 仍携带 num_heads，即 [q_len, n * (qk_nope_dim + qk_rope_dim)]。也就是说，我们通过改变乘法的顺序，可以让 k/v 不展开，减少了张量 load 压力。考虑到 deepseek 类模型结构中 num_heads 通常为 128。因此，相较于正常模式，K/V tensor 的访问规模可扩大 42.6 倍。

计算公式如下：

$$\frac{n*(qk\_nope\_dim + qk\_rope\_dim)}{kv\_lora\_rank + qk\_rope\_dim}=\frac{128 * (128+64)}{512 + 64}=42.6$$

---

下面的是不准确的，一开始被矩阵吸收这个词误导，误以为是“权重的提前计算合并”：

不会，可以通过一些巧妙的数据公式推导，将很多权重的计算合并为一个。下面具体解释一下操作。

先来回顾上面的公式（4）和（5）：

$$\{k^C_t, k^R_t\}=\{W^{UK}c^{KV}_t,\operatorname{RoPE}(W^{KR}h_t)\}$$

$$v^C_t=W^{UV}c^{KV}_t$$

当我们缓存了 $c^{KV}_t$ 后，从上面公式看，似乎我们在每次推理的时候都必须重新计算 $k_t$ 和 $v_t$。但其实不然，这些计算可以在计算 $q^T_{t,i}k_{t,i}$ 时被合并起来，最终效果就是我们并不需要显式的计算出 $k_{t,i}$ 和 $v_{t,i}$，只需要将公式（1）和公式（4）代入到公式（6）的，再整理一下即可：

$${q^C_t}^Tk^C_t=(W^{UQ}c^Q_t)^TW^{UK}c^{KV}_t={c^Q_t}^T{(W^{UQ})}^TW^{UK}c^{KV}_t={c^Q_t}^TWc^{KV}_t \tag{8}$$

可以看到，我们在推理时，可以先计算（或者说直接存储该权重） $W={(W^{UQ})}^TW^{UK}$
，这样就避免了多次矩阵计算，从而达到既克服 KV Cache过大的问题，又可以减少计算的效果。

但我们还要考虑 RoPE 的部分，就是 $q^R_t$ 和 $k^R_t$，他们带了 RoPE 计算，没有办法直接做此类合并，因为 RoPE 和矩阵乘不满足乘法交换律：

$$k^R_t=\operatorname{RoPE}(W^{KR}h_t)\neq W^{KR}\operatorname{RoPE}(h_t) \tag{9}$$

也就是说，如果我们的 QK 带了 RoPE 运算，那么公式（8）里的小技巧就无法实现了，我们需要老老实实一步步计算出所有的矩阵，这是我们不愿意看到的。

这就是 MLA 作者的点睛之笔。MLA 在设计时，仅对部分 QK 做 RoPE（这里有个假设必须成立，即位置编码信息应用到部分而非全局也可以 work），然后对做了 RoPE 的 QK 做分开计算：

$$q^T_{t,i}k_{j,i}=\begin{bmatrix} {c^Q_t}^T(W^{UQ})^T & (q^R_t)^T \end{bmatrix} \begin{bmatrix} W^{UK}c^{KV}_t \\ k^R_t \end{bmatrix}={c^Q_t}^TWc^{KV}_t+(q^R_t)^Tk^R_t \tag{10}$$

即对所有 query，前面的 $d_h=128$ 维都是不带位置编码信息的，而另外$\frac{1}{2}d_h=64$维则是带旋转位置编码信息的。于是，此时我们仍然能把一部分的 QK 计算简化。当然对于有 RoPE 的矩阵，就要一步一步算了。

小结

Multi-Head Latent Attention (MLA) 通过的使用低秩矩阵，减少了推理时的 KV Cache，同时保持了与标准多头注意力机制相当的性能。此外，MLA 中采用对部分 QKV 做 RoPE 的方法，既保留了 QKV 中的位置编码信息，又可以减少计算次数，提升推理效率。

附：DeepSeek-V3 论文中对 DeepSeek v3 架构的解释图。其中下半部分为本文解释的 MLA 机制。

MoE 架构

接下来我们看一下 DeepSeek-V3 的 MoE 架构。目前，其他许多模型也使用了 MoE(Mixture of Experts) 架构，MoE 架构中包含多个“专家”网络，每个专家专注于处理特定类型的输入或特征。当一个输入进来时，会有一个 Gate 决定将输入路由到哪些最合适的专家进行处理。这样做的好处是，在推理时可以部分激活专家权重，从而减少推理时感知层的计算量。这样一来，模型就能不受限于推理速度，可以进一步做大，包含更多数据信息。

以 DeepSeek-V3 为例，MoE 层主要由两种类型的专家构成：

• 路由专家 (Routed Experts): 数量众多，负责处理特定类型的输入。DeepSeek-V3 的每个 MoE 层包含 256 个路由专家。
• 共享专家 (Shared Experts): 数量较少，负责处理所有输入，提供通用的特征提取。DeepSeek-V3 每个 MoE 层包含 1 个共享专家。

下面我给出这张流程图，详细介绍 vllm 中 deepseek 的 MoE 执行过程：

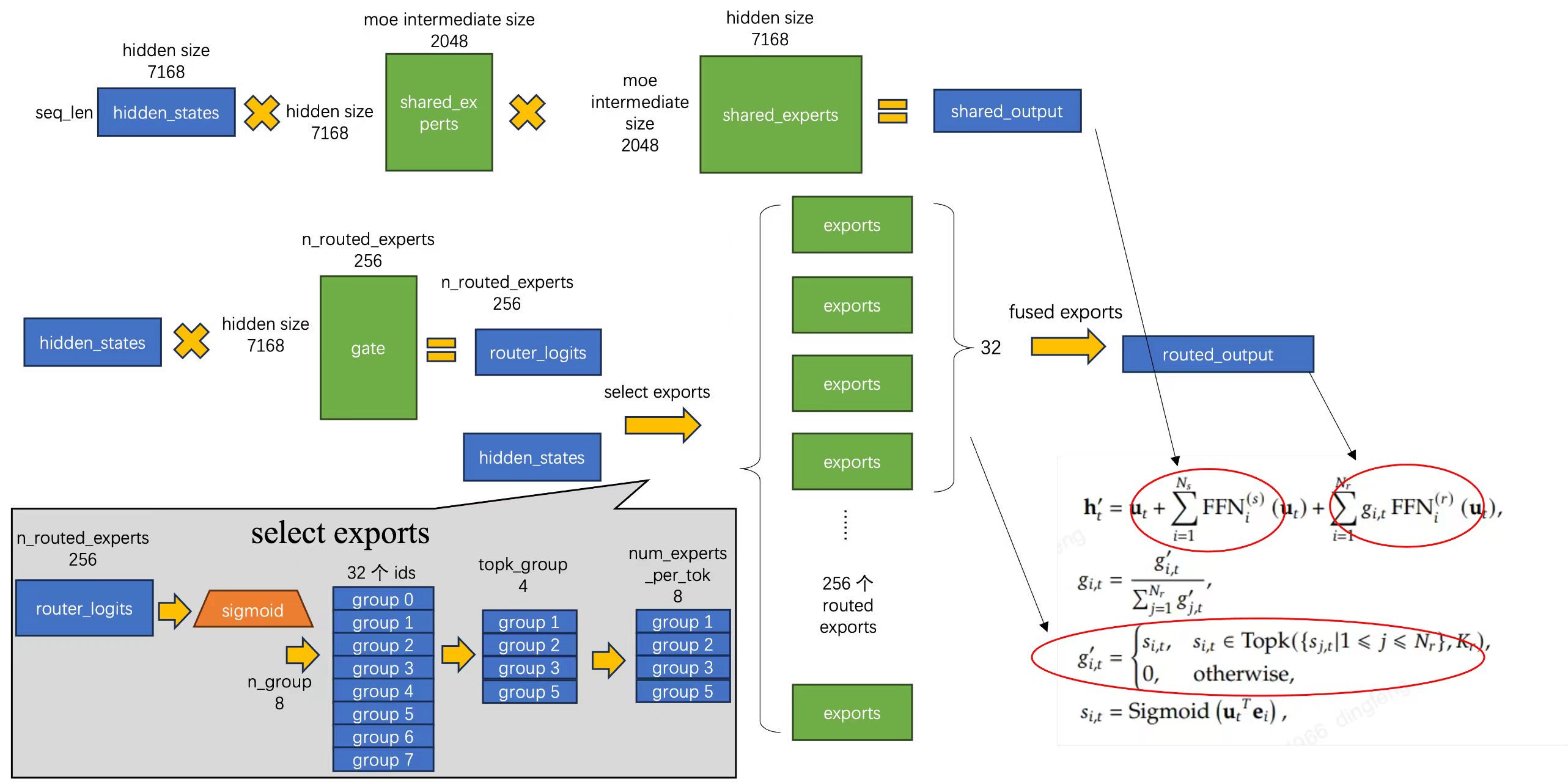
1. 首先，MoE 架构包括了 Shared Exports 和 Routed Exports，上边的路线走了共享专家路线，每个 $u_t$ 都需要计算该路线，得到 $\sum^{N_s}_{i=1}{\operatorname{FFN}^{(s)}_i(u_t)}$
2. 然后就是路由专家的路线。首先，hidden states 需要走过一个 Gate 矩阵，计算出 256 个 专家的 gates 值，该 gates 值用于选取专家做推理计算。具体过程在 select exports 中展现：
3. routed logits 经过激活函数后，将 256 个 logits 分成 8 组，每组 32 个，然后使用 topk 函数排序，将最大的其中 4 个取出。
4. 取出最大的 4 个 group 后，从每个 group 中再取出最大的 8 个，最后得到 32 个 exports 网络，再用 gates 和 FFN 计算出结果，得到 $\sum^{N_r}_{i=1}{g_{i,t}\operatorname{FFN}^{(r)}_i(u_t)}$