深入 CUTLASS 之 CuTe 详解

什么是 CuTe

CuTe 就是 CUDA Tensor。更准确地说，是 nvidia 在 CUTLASS 3.0项目中开发并提供的一组 C++ CUDA Template 抽象工具，它主要用于定义和操作在 CUDA 中的有多维分层 layout 的线程和数据。

CuTe 最主要的概念就是 Layout 和 Tensor：

Layout<Shape, Stride> 可以把它理解成 function，作用就是将 n 维的连续坐标映射到 1 维的存储空间中
Tensor 有了 Layout 之后，就可以将指针传给 Tensor，于是 Tensor 就可以用来做计算了！

此外，还需要特别注意的是，对于一个同样的连续地址空间，使用不同的 Layout 可以让 Tensor 的维度和排布不同。这就给了 CuTe 很大的灵活性，让它能够处理复杂的地址变换，帮助程序员摆脱 CUDA 编程中繁琐复杂的数据线程排布，让程序员可以专注于算法的逻辑描述。

当然，程序员也不太可能完全不关系数据（或线程）的排布方式，CuTe 也提供了许多健壮的 API 来帮助程序员更好地操控数据。

在真正的效果面前，文字都是苍白的。我们来看个具体的例子：

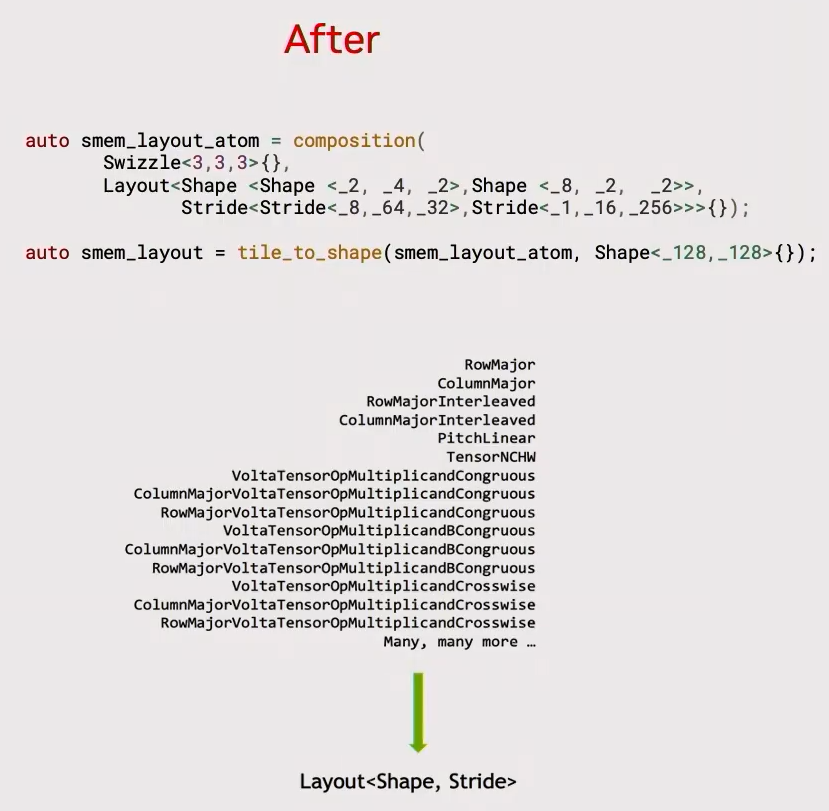
在 CuTe 之前，我们为了高性能地执行 CUDA 并行，需要花费大量时间在理解每个线程和线程块要处理哪部分数据，最终写出左边的“丑陋代码”：不仅不易阅读理解，更不容易调试和维护；而在 CuTe 之后，只要程序员掌握了它的 API，并正确地理清数据和线程的布局，准确地使用 layout 等模板类，代码可读性就能大幅提高了，也更容易调试修改。

轻松驾驭 CuTe 也绝非易事。首先，它用大量天书般的 C++ Template 编写，因此需要程序员有扎实的 C++ 功底；其次由于 CuTe 的核心抽象是分层地多维 layout，并且它必须足够强大到表示 CUDA 并行计算时的几乎一切操作，这也意味着有时要理解它也十分困难。总之，CuTe 的学习曲线非常陡峭，一点都不 cute ！

本博客致力于和大家一起探讨 CuTe 的相关使用，尽可能降低学习曲线。

在开始前，还是提醒各位读者，若有不明白的地方，可以速览参考官方文档。

Layout

Layout 是 CuTe 的核心抽象，弄懂了 Layout 就基本学会了一半 CuTe。Layout 概念提供了一种快速找到多维数据与坐标的映射关系，使得程序员更好地操作线程做并行运算，其本质就是如何快速地将“多维”坐标映射在“一维”的内存上，因此也可以说：

Layouts 是整数（逻辑一维坐标）到整数（一维索引）的函数
Layouts are functions from integers to integers.

从例子开始

先来看几个使用 Layout 来摆布数据的例子，直观地感受一下 CuTe Layout：

例一

#include <cute/tensor.hpp>
// ...
  auto tensor_shape = make_shape(2, 3);
  auto tensor_stride = make_stride(1, 2);
  print_layout(make_layout(tensor_shape, tensor_stride));

输出结果：

(2,3):(1,2)
      0   1   2 
    +---+---+---+
 0  | 0 | 2 | 4 |
    +---+---+---+
 1  | 1 | 3 | 5 |
    +---+---+---+

(2,3):(1,2) 中前面的括号表示 Tensor 的形状，后面的括号表示在不同维度下的 Stride。这里我们定义了一个 2x3 的 tensor，2 行 3 列。至于 stride，在前一维度（行维度），stride=1，表示映射到一维空间中，按行方向递增时，stride +1；在后一维度（列维度），stride=2，表示映射到一维空间中，按列方向递增时，stride +2。

例二

1
2
3

tensor_shape = make_shape(2, 3);
tensor_stride = make_stride(3, 1);
print_layout(make_layout(tensor_shape, tensor_stride));

输出结果：

(2,3):(3,1)
      0   1   2 
    +---+---+---+
 0  | 0 | 1 | 2 |
    +---+---+---+
 1  | 3 | 4 | 5 |
    +---+---+---+

定义了一个 2x3 的 tensor，2 行 3 列。至于 stride，在前一维度（行维度），stride=3，表示映射到一维空间中，按行方向递增时，stride +3；在后一维度（列维度），stride=2，表示映射到一维空间中，按列方向递增时，stride +1。

例三

1
2
3

Layout layout = make_layout(make_shape (make_shape (2,2), 2),
                            make_stride(make_stride(4,2), 1));
print_layout(layout);

输出结果：

((2,2),2):((4,2),1)
      0   1 
    +---+---+
 0  | 0 | 1 |
    +---+---+
 1  | 4 | 5 |
    +---+---+
 2  | 2 | 3 |
    +---+---+
 3  | 6 | 7 |
    +---+---+

可以这样理解，在行维度上，我们有未知的子 tensor，该子 tensor 有两行（此为 shape 第一个2），行之间的 stride 为 4（所以 stride 第一个数为 4）；然后该子 tensor 在整个大 tensor 中会重复两次（此为 shape 的第二个 2），相对应地，子 tensor 间的 stride 为 2（此为 stride 的第二个 2）。

例四

1
2
3

Layout layout = make_layout(make_shape (8,make_shape (2,2)),
                            make_stride(2,make_stride(1,16)));
print_layout(layout);

输出结果：

(8,(2,2)):(2,(1,16))
       0    1    2    3 
    +----+----+----+----+
 0  |  0 |  1 | 16 | 17 |
    +----+----+----+----+
 1  |  2 |  3 | 18 | 19 |
    +----+----+----+----+
 2  |  4 |  5 | 20 | 21 |
    +----+----+----+----+
 3  |  6 |  7 | 22 | 23 |
    +----+----+----+----+
 4  |  8 |  9 | 24 | 25 |
    +----+----+----+----+
 5  | 10 | 11 | 26 | 27 |
    +----+----+----+----+
 6  | 12 | 13 | 28 | 29 |
    +----+----+----+----+
 7  | 14 | 15 | 30 | 31 |
    +----+----+----+----+

同理可知道，在列方向上，Shape 的第一个 2 表示，列内的子 tensor pattern 有两列，第二个 2 表示列一共有两个子 pattern 。Stride 的 1 表示在这个子 pattern 内的 stride 为 1，16 表示子 pattern 间的 stride 为 16。

基本类型和概念

相信前面的三个例子给到了读者对 Layout 的一个基本理解。因此在本小节中，我们来系统地梳理一下 CuTe Layout。

Tuple

CuTe 以元组（tuple）为起始，cute::tuple 包含了若干个元素组成的有限序列元组，其行为与 std::tuple 类似，但引入了一些 C++ templates arguments 的限制，并削减了部分实现以提升性能。

IntTuple

cuTe 还定义了 IntTuple 概念。为的就是实现上面例三、例四中令大家一时感到费解的 make_shape 嵌套。

1	`make_shape (make_shape (2,2), 2)`

IntTuple 既可作为一个整数，也可作为一个 Tuple 类型。这个递归定义允许我们构建任意嵌套的 Layout。以下任何一个都是 IntTuple 的有效模板参数：

int{2} 运行时整数，或者称之为动态整数，就是 C++ 的正常整数类型比如 int size_t 等等，只要是 std::is_integral<T> 的都是
Int<3>{} 编译期整数，或称之为静态整数。CuTe 通过 cute::C<Value> 来定义 CUDA 兼容的静态整数类型，使得这些整数的计算能在编译期内完成。CuTe 将别名 _1、_2、_3等定义为 Int<1>、Int<2>、Int<3>等类型。
带有任何模板参数的 IntTuple，比如 make_tuple(int{2}, Int<3>{})

CuTe 不仅将 IntTuple 用在了 Layout 上，还会在很多其他的地方比如 Step 和 Coord 等用到它。

IntTuple 的相关 API 操作：

rank(IntTuple): 返回 IntTuple 的元素个数
get<I>(IntTuple): 返回 IntTuple 的第Ith 个元素
depth(IntTuple): 返回 IntTuple 的嵌套层数，整数为 0
size(IntTuple): 返回 IntTuple 中所有元素的乘积。

Layout 的使用

Layout 本质上就是由一对 IntTuple 组成，Shape 和 Stride。Shape 定义了 Tensor 的大小，Stride 定义了元素间的距离。因此 Layout 也有许多与 IntTuple 类似的操作：

rank(Layout): Layout 的维度，等同于 Shape 的 rank(IntTuple)
get<I>(Layout): 返回 Layout 的第 Ith 个元素
depth(Layout): 返回 Layout 的嵌套层数，整数为 0
shape(Layout): The shape of the Layout
stride(Layout): The stride of the Layout
size(Layout): 返回 Layout 中所有元素的乘积。等同于 size(shape(Layout))
cosize(Layout): The size of the Layout function’s codomain (not necessarily the range). Equivalent to A(size(A) - 1) + 1

Layout 坐标与索引

刚才我们给出的例子都是二维的矩阵，事实上一维 vector 也是可以用 CuTe 表示的，只不过 Layout 维度 rank == 1。例如，Layout 8:1 就是 8 个元素的连续 vector

1
2
3

Layout:  8:1
Coord :  0  1  2  3  4  5  6  7
Index :  0  1  2  3  4  5  6  7

这里我们开始引入 Coord 坐标来表示数据在 Tensor 的相对位置。使用 index 索引来表示数据在内存上的位置，使用 print_layout 打印出来的都是 index。

相似的，Layout 8:2 中，Coord 是不变的（仍然是 8 个元素），但 index 因为 Stride 为 2，内存上会空一个存一个数据：

1
2
3

Layout:  8:2
Coord :  0  1  2  3  4  5  6  7
Index :  0  2  4  6  8 10 12 14

所有的多维矩阵在内存上都是一维存储的。要想将二维 Layout 要转化为一维 vector ，需要在最外层套上一层括号，即将 (4,2):(2,1) 改写为 ((4,2)):((2,1))。顺序是列主序，从第一列开始拆解，从上到下从左到右一个个按序写入：

Layout:  ((4,2)):((2,1))
      0   1 
    +---+---+
 0  | 0 | 1 |
    +---+---+
 1  | 2 | 3 |
    +---+---+
 2  | 4 | 5 |
    +---+---+
 3  | 6 | 7 |
    +---+---+
Coord :  0  1  2  3  4  5  6  7
Index :  0  2  4  6  1  3  5  7

Layout:  ((4,2)):((1,4))
      0   1 
    +---+---+
 0  | 0 | 4 |
    +---+---+
 1  | 1 | 5 |
    +---+---+
 2  | 2 | 6 |
    +---+---+
 3  | 3 | 7 |
    +---+---+
Coord :  0  1  2  3  4  5  6  7
Index :  0  1  2  3  4  5  6  7

除了简单的数字坐标外，还有更复杂更易理解的多维坐标。之前提过，一维坐标是将矩阵以列主序的方式从上到下从左到右；二维坐标则使用行号列号两个数字做寻找，而自然坐标则与 tensor layout 的形式完全一致。数学上，自然坐标与 Stride 做内积可以得到 index 索引。

Layout (3, (2, 3)):(3, (12, 1))
       0     1     2     3     4     5     <== 1-D col coord
     (0,0) (1,0) (0,1) (1,1) (0,2) (1,2)   <== 2-D col coord (j,k)
    +-----+-----+-----+-----+-----+-----+
 0  |  0  |  12 |  1  |  13 |  2  |  14 |
    +-----+-----+-----+-----+-----+-----+
 1  |  3  |  15 |  4  |  16 |  5  |  17 |
    +-----+-----+-----+-----+-----+-----+
 2  |  6  |  18 |  7  |  19 |  8  |  20 |
    +-----+-----+-----+-----+-----+-----+
对于Tensor中的索引 17，有如下坐标
Coord: 16
Coord: (1, 5)
Coord: (1, (1, 2))

在 CuTe 中，可使用 idx2crd 将索引转换到坐标：

auto shape = Shape<_3,Shape<_2,_3>>{};
print(idx2crd(   16, shape));                                // (1,(1,2))
print(idx2crd(_16{}, shape));                                // (_1,(_1,_2))
print(idx2crd(make_coord(   1,5), shape));                   // (1,(1,2))
print(idx2crd(make_coord(_1{},5), shape));                   // (_1,(1,2))
print(idx2crd(make_coord(   1,make_coord(1,   2)), shape));  // (1,(1,2))
print(idx2crd(make_coord(_1{},make_coord(1,_2{})), shape));  // (_1,(1,_2))

亦可使用 crd2idx 将坐标转换为索引：

auto shape  = Shape <_3,Shape<  _2,_3>>{};
auto stride = Stride<_3,Stride<_12,_1>>{};
print(crd2idx(   16, shape, stride));       // 17
print(crd2idx(_16{}, shape, stride));       // _17
print(crd2idx(make_coord(   1,   5), shape, stride));  // 17
print(crd2idx(make_coord(_1{},   5), shape, stride));  // 17
print(crd2idx(make_coord(_1{},_5{}), shape, stride));  // _17
print(crd2idx(make_coord(   1,make_coord(   1,   2)), shape, stride));  // 17
print(crd2idx(make_coord(_1{},make_coord(_1{},_2{})), shape, stride));  // _17

CuTe 还支持 Tensor 的一维或多维索引，在本例中，如果我们要索引到 5 这个数字，那么可以通过 Tensor(4) 或者 Tensor(1, 1) 来获得。我们来看一个更复杂的例子

Layout 兼容

如果布局A和布局B的形状是兼容的，那么它们就是兼容的。如果A的任何自然坐标也是B的有效坐标，则形状A与形状B兼容。

Flatten
“Flatten”操作“un-nest”可能嵌套的Layout。例如

Layout 代数学

#AI #CUTLASS

深入 CUTLASS 之 CuTe 详解

https://dingfen.github.io/2024/08/18/2024-8-18-cute/

作者

Bill Ding

发布于

2024年8月18日

更新于

2024年9月24日

许可协议

VLLM Paged Attention 实现下一篇