CUDA 中的向量内积

博主本科时略学过 CUDA 编程的相关知识，但远算不上熟练，更谈不上精通。恰好本人对并行计算很感兴趣，这几天实现了一下最基础的向量内积，对以前的知识做了一点总结，算是温故而知新，可以为师矣。

向量内积

两个长为 N 的向量做内积。从并行计算的角度看，可并行部分就是 a[i] * b[i] 部分，然后再对得到的乘积做累加求和。可以让 GPU 中的每个线程执行一个 a[i] * b[i]，然后再进行累加。如下图，考虑到 N 可能非常大，GPU 网格中的线程数量不足以覆盖整个向量，因此需要使用 while 循环，让线程运算多个乘法。

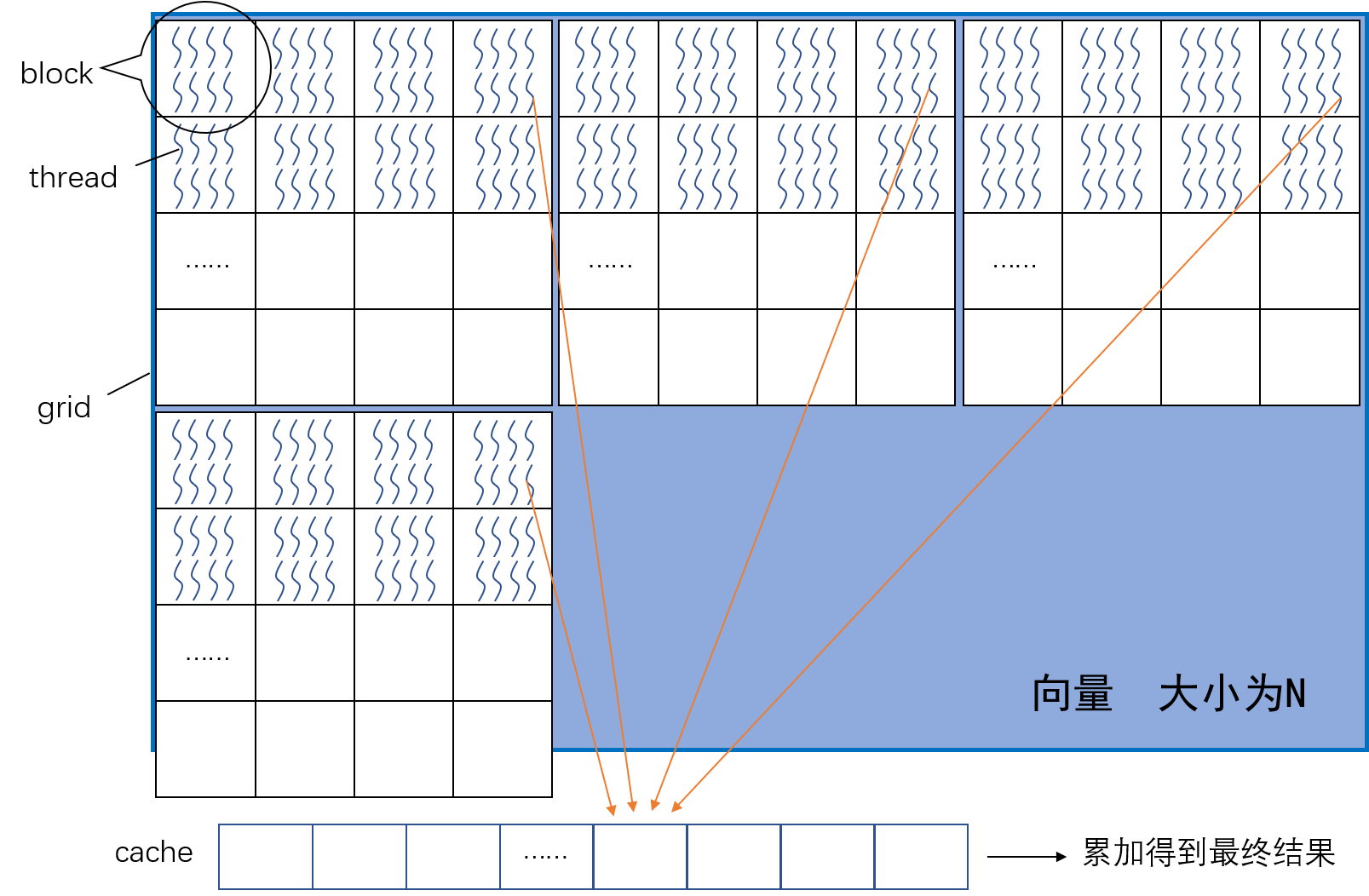
具体而言，在下面的这个循环中，每个线程都会运行一个 grid 中的一次乘法，然后跳转到下一个 grid 继续完成乘法。因此，程序的 while 循环，让每个线程计算相应的乘法后，跨越一个 grid 的长度再完成乘法，最后累加到 cache 数组中（橙色箭头），为了不让自增的 tid 变量超过数组边界，每次累加后还需要在 while 语句中判断一下。相应的代码如下，配合上图相应能更好地理解计算过程。

__global__ void dot(float *c, float *a, float *b) {
  int tid = threadIdx.x + blockIdx.x * blockDim.x;
  float cache[blockDim.x * gridDim.x];
  float ans = 0.0f;
  // 线程并行地执行内积 乘法
  while(tid < N) {
    ans += a[tid] * b[tid];
    tid += blockDim.x * gridDim.x;
  }
  cache[threadIdx.x + blockIdx.x * blockDim.x] = ans;

上述计算完成后，还需要将 cache 中的数组进一步累加。但这里必须注意，进一步累加前，必须确保所有线程已经完成了上面的循环。因此，这里需添加一个 barrier：

// 线程同步，确保所有线程都完成了上面的循环
__syncthreads();

随后，使用一个线程对 cache 中的数组累加，输出结果。

// 归约累加
float sum = 0.0f;
if (tid == 0) {
  for(int i = 0; i < gridDim.x * blockDim.x; i++) {
    sum += cache[i];
  }
  printf("dot product is : %f\n", sum);
}

程序优化

上述代码虽然可以完成任务，但没有达到更高的性能。下面我对上面的程序做进一步优化。

首先介绍一下 CUDA C 中的共享内存。共享内存中的变量被线程块中的每个线程共享，而其他线程不能对其访问和修改。要使用共享内存，在编写 CUDA 代码时，只需要注意将共享内存和线程块“捆绑”考虑就行。共享内存可以让一个线程块中的线程更快地完成通信协作，执行更加复杂的任务。最后，共享内存在物理上更贴近线程，因此访问共享内存时的延迟要远低于访问普通缓冲区的延迟。

但在使用线程之间的通信时，还需要注意线程之间的同步，防止出现竞争条件（Race Condition），避免错误。

回到该问题，可以明显看到，while 循环中计算出的结果完全可以暂存到共享内存中。而由于共享内存是被一个线程块内的线程共享的，因此 cache 的大小也要改为线程块的大小，而不是整个网格的大小：

__global__ void dot(float *c, float *a, float *b) {
  int tid = threadIdx.x + blockIdx.x * blockDim.x;
  __shared__ float cache[blockDim.x];
  float ans = 0.0f;
  // 线程块内的线程并行地执行内积 乘法
  while(tid < N) {
    ans += a[tid] * b[tid];
    tid += blockDim.x * gridDim.x;
  }
  cache[threadIdx.x] = ans;

改为共享内存后，后面的归约累加部分也必须更改。因为 0 号线程不可能访问其他线程块的共享内存。因此，需要在线程块中完成累加。具体做法类似于[二叉树求和](https://dingfen.github.io/Parallel Computing/2020/12/17/PP02.html#%E4%BA%8C%E5%8F%89%E6%A0%91%E6%B1%82%E5%92%8C%E5%AE%9E%E7%8E%B0)。每个线程将数组的两个值加起来，再将结果写到低索引位的数上。这样一次循环结束后，数组中的有效数据便只剩下一半。下一个循环再对这一半数组做同样操作，依次往复，直到累加值存在于 cache[0] 中。但注意：这种算法要求线程块内线程数量必须为 2 的幂次。

int i = blockDim.x / 2;
while(i != 0) {
  if (threadIdx.x < i)
    cache[threadIdx.x] += cache[threadIdx.x + i];
  __syncthreads();  // 为何一定要加上？
  i /= 2;
}

if (threadIdx.x == 0)
  c[blockIdx.x] = cache[0];

很遗憾核函数只能做到这一步了，因为 cache[0] 都存在于共享内存中，GPU 中没有一个线程可以访问到所有的结果，所以进一步的累加只能靠 CPU。但别灰心，提前放弃在 GPU 中的计算事实上是一件好事：因为累加求和的归约运算一般只能由一个线程完成，交给 GPU 做只能说是杀鸡用牛刀，太浪费计算资源。而且，此时数据量已经非常小，CPU 也能很出色地完成任务。

// last reduction for cpu
for (int i = 0; i < blocksPerGrid; i++) {
  *ans += c[i];
}

最后，放上核函数及其调用代码，供大家参考。若想亲自实验，可从github 链接获取。

__global__ void dot(float* c, float* a, float* b) {
  __shared__ float cache[threadsPerBlock];
  int tid = threadIdx.x + blockIdx.x * blockDim.x;
  int cacheIndex = threadIdx.x;
  // gird loops addition, reduce sum in cache for every thread.
  float temp = 0.0;
  while (tid < N) {
    temp += a[tid] * b[tid];
    tid += blockDim.x * gridDim.x;
  }
  cache[cacheIndex] = temp;
  // thread synchronize
  __syncthreads();

  // Reductions parallel as Binary tree in each block
  int i = blockDim.x / 2;
  while (i != 0) {
    if (cacheIndex < i)
      cache[cacheIndex] += cache[cacheIndex + i];
    __syncthreads();
    i /= 2;
  }

  if (cacheIndex == 0)
    c[blockIdx.x] = cache[0];
  // for not waste computing resource, exit now.
}

extern "C" cudaError_t dotproduct(float* ans, float* a, float* b) {
  float* dev_a = NULL;
  float* dev_b = NULL;
  float* dev_c = NULL;
  float* c = NULL;
  float time;
  
  c = (float*)malloc(blocksPerGrid * sizeof(float));
  cudaEvent_t start, stop;
  GPUAssert(cudaEventCreate(&start));
  GPUAssert(cudaEventCreate(&stop));
  GPUAssert(cudaEventRecord(start, 0));
  GPUAssert(cudaMalloc(&dev_a, N * sizeof(float)));
  GPUAssert(cudaMalloc(&dev_b, N * sizeof(float)));
  GPUAssert(cudaMalloc(&dev_c, blocksPerGrid * sizeof(float)));

  GPUAssert(cudaSetDevice(0));

  GPUAssert(cudaMemcpy(dev_a, a, N * sizeof(float), cudaMemcpyHostToDevice));
  GPUAssert(cudaMemcpy(dev_b, b, N * sizeof(float), cudaMemcpyHostToDevice));

  dot<<<blocksPerGrid, threadsPerBlock>>>(dev_c, dev_a, dev_b);

  GPUAssert(cudaGetLastError());
  GPUAssert(cudaDeviceSynchronize());
  GPUAssert(cudaMemcpy(c, dev_c, blocksPerGrid * sizeof(float), cudaMemcpyDeviceToHost));

  GPUAssert(cudaEventRecord(stop, 0));
  GPUAssert(cudaEventSynchronize(stop));
  GPUAssert(cudaEventElapsedTime(&time, start, stop));
  // last reduction for cpu
  for (int i = 0; i < blocksPerGrid; i++) {
    *ans += c[i];
  }

  printf("GPU time: %8.4f\n", time);
  cudaFree(dev_a);
  cudaFree(dev_b);
  cudaFree(dev_c);
  cudaEventDestroy(start);
  cudaEventDestroy(stop);
  free(c);
  return cudaSuccess;
}

kahan 算法

更新于 2023.9.4

闲来无事，重新温故一下几年前写的代码。突然发现，这好像没算对啊，CPU 计算出来的数据跟 GPU 的数据怎么都对不上。只要数据量一大（上千），二者得出的结果就会差几十，数据量越大差得越多，为啥呢？

首先，我反复琢磨了这几行几年前写的代码，反反复复地推导后得出结论：根本没问题。那么问题出在哪里？

问题出在：浮点数的加法不满足结合律。用数学的话说，即 $$ (a+b)+c \neq a+(b+c) $$。为什么会这样？这得从浮点数在计算机中的表示说起，在计算机程序中，我们需要用有限位数对实数做近似表示，如今的大多数计算机都使用 IEEE-754 规定的浮点数来作为这个近似表示。然而一旦扯到这个，其篇幅和知识点不是本博客可以接受的了的，因此这里就放个链接供各位感兴趣的读者自行研究。

跳过这些复杂繁琐的细节，这里直接给出了结论：因计算机内资源有限，浮点数在其中无法被精确表示，导致绝对值越大的浮点数拥有越不精确（越少）的小数点位数，而绝对值越接近于0的数有更多的精确的小数点位数。为方便理解，各位读者可以简单地用 C++ 运行如下算式，看它们的结果是否相等。然后再把 float 变为 double，或者减小数字的绝对值等，看结果是否有变化。

float s1 = (100000000.00001f - 100000000.f) + 0.00001f;
float s2 = (100000000.00001f + 0.00001f) - 100000000.f;

那么这跟咱们的程序无法得到准确结果有什么关系呢？首先，因为我们在计算两个甚长向量的内积值，这意味着在算数的最后，我们需要将很多浮点乘积值逐一累加起来，具体做法就是一个一个地将乘积值加入到前缀和中。而若这些乘积值都是正浮点数（或者负浮点数），那么不断累加后，其前缀和的绝对值必然会变得越来越大。而前面提到过，由于计算机内表示一个浮点数所用的资源有限，为表示该前缀和，计算机不得不丢掉越来越多的小数点后的位数，导致该值也就越来越不精确。甚至到最后，前缀和再继续累加乘积值后，可能由于乘积值过小而直接被抛弃了！

计算机运算浮点数存在了这种精度缺陷，应当如何解决？想必大家能从上面的例子中获得一些启发：适当地交换运算顺序，或许就能够避免因“大数加小数”产生的精度损失。kahan 求和法便是利用了这一特点，尽可能挽救了因不断累加而丢失的精确度。

在介绍 kahan 求和法前，先明确一下我们要解决的问题：有一个内含大量正浮点数的数组 nums，需求得其总和。在不断累加的过程中，我们用 sum 表示中间过程的前缀和。显然，程序执行到一定程度后，必然会出现 sum 很大，而 nums 内值很小的情况。因此若直接计算 sum += nums，则 nums 的小数点低位数会丢失。而 kahan 求和法通过记住这其中的误差，将其加到后续的结果中，即可挽回损失的精度。

具体是这样做的，已知 sum += num 是不准确的，产生了 eff 的误差。此时考虑：c = (sum + num) - sum - num。注意，关于 c 的计算中，只有 sum + num 是不准确的（因为只有这个运算涉及到了大数加小数），因此，c 可以将加法产生的误差保留下来，近似等于 eff。此外，针对 c 的运算顺序不能变化！否则就有不止一个运算是不准确的了。我们保留 c，在计算下一个加法的时候，再将这个误差补上，更新到 sum 中去。

Kahan 求和算法主要通过一个单独变量 c 用来累积误差。如下方参考代码所示：

float kahanSum(vector<float> nums) {
  float sum = 0.0f;
  float c = 0.0f;
  for (auto num : nums) {
    float y = num - c;
    float t = sum + y;
    c = (t - sum) - y;
    sum = t;
  }
  return sum;
}

注：Kahan 求和法，又名补偿求和或进位求和法，是一个用来降低有限精度浮点数序列累加值误差的算法。它主要通过保持一个单独变量用来累积误差（常用变量名为 c）来完成的。该算法主要由 William Kahan 于 1960s 发现。因为 Ivo Babuška 也曾独立提出了一个类似的算法，Kahan 求和算法又名为 Kahan–Babuška 求和算法。