深入理解计算机系统之代码优化实验

深入理解计算机系统之代码优化

实验介绍

图像处理中存在很多函数，可以对这些函数进行优化。本实验主要关注两种图像处理操作

旋转：对图像逆时针旋转90度
平滑：对图像进行模糊操作

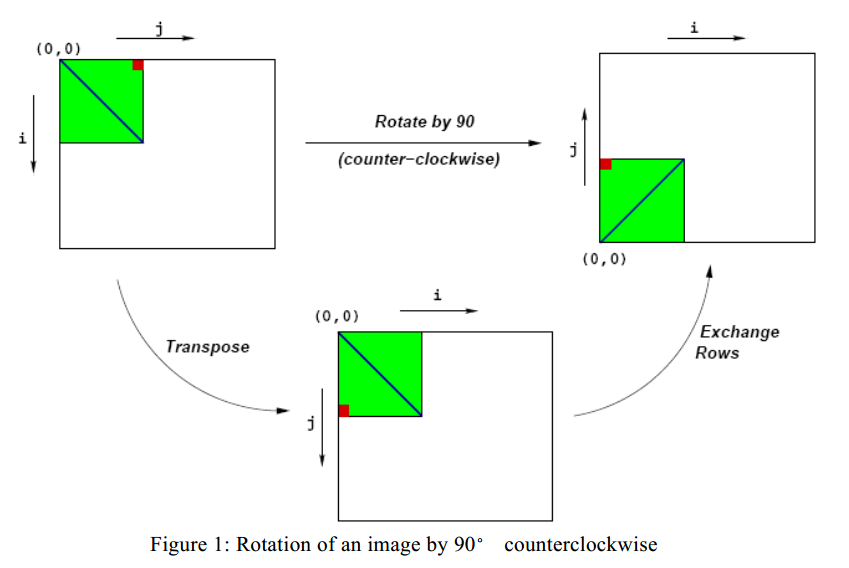
若图像用二维矩阵 $M$ 表示， $M_{ij}$ 表示图像 $M$ 的第 $(i, j)$ 像素的值，像素值用红，绿，蓝表示。我们只会考虑方形图像。令N表示图像的行（或列）数，从0到N − 1编号。给定这种表示形式，旋转操作可以非常简单地实现为以下两个矩阵运算：

转置：对于每对 $(i, j)$ ， $M_{i , j}$ 和 $M_{j, i}$ 是互换的
交换行：第i行与第N-1 − i行交换。

旋转操作的具体步骤如下图所示：

平滑操作的目标是将每个像素值改为其周围像素值的平均值。参考以下公式：

M2[1][1]=\frac{\sum^2_{i=0}\sum^2_{j=0}M1[i][j]}{9}

M2[N−1][N−1]=\frac{\sum^{N−1}_{i=N−2}\sum^{N−1}_{j=N−2}M1[i][j]}{4}

代码优化

本次实验中，我们需要修改唯一文件是 kernels.c。driver.c 是驱动程序，使我们修改的程序能运行，并对其进行评分。使用命令 > make driver 生成驱动程序代码，并使用 ./driver 命令运行它。

数据结构体

图像的核心数据是用结构体表示的。像素是一个结构，如下所示：

typedef struct {
    unsigned short red; /* R value */
    unsigned short green; /* G value */
    unsigned short blue; /* B value */
} pixel;

可以看出，RGB 是 16 位表示形式。图像 M 表示为一维像素阵列，那么在代码中，可以用M[RIDX(i,j,n)] 表示第 $(i, j)$ 个像素。这里n是图像矩阵的维数，RIDX是定义如下的宏：

1	`#define RIDX(i,j,n) ((i)*(n)+(j))`

旋转操作

以下 C 函数计算将源图像旋转90°，并将结果存储在目标图像中。

void naive_rotate(int dim, pixel *src, pixel *dst) {
    int i, j;
    for(i=0; i < dim; i++)
    	for(j=0; j < dim; j++)
    		dst[RIDX(dim-1-j,i,dim)] = src[RIDX(i,j,dim)];
    return;
}

从下图可以看出，旋转操作必然会在一定程度上违反局部性原理。因此我首先想到的是，把循环分块，好让高速缓存能完全容纳一个小循环内所需要访问的数据，增强程序的局部性。

分别以8*8分块、16*16分块和32*32分块做测试，代码都很类似，仅将8*8代码放置下方。

void rotate_8x8(int dim, pixel *src, pixel *dst) {
    int i, j;

    for(int i1 = 0; i1 < dim; i1+=8)
    for(int j1 = 0; j1 < dim; j1+=8)
    for (i = i1; i < i1+8; i++)
	    for (j = j1; j < j1+8; j++)
	        dst[RIDX(dim-1-j, i, dim)] = src[RIDX(i, j, dim)];
}

经过测试，得出的结果如下：

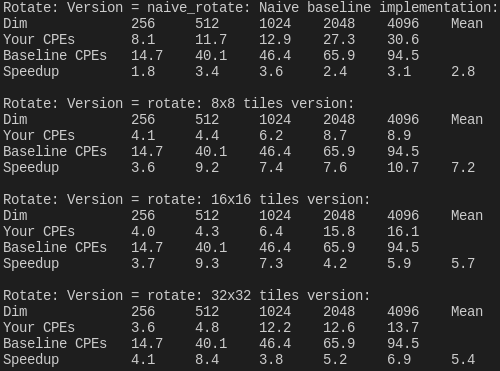
从结果看，8*8的分块获得的优化性能最好，而随着分块越大，性能就会变得越差。

平滑操作

简而言之，就是要对如下代码进行优化：

void naive_smooth(int dim, pixel *src, pixel *dst) {
    int i, j;
    for(i=0; i < dim; i++)
    for(j=0; j < dim; j++)
    dst[RIDX(i,j,dim)] = avg(dim, i, j, src); /* Smooth the (i,j)th pixel */
    return;
}

static pixel avg(int dim, int i, int j, pixel *src) 
{
    int ii, jj;
    pixel_sum sum;
    pixel current_pixel;

    initialize_pixel_sum(&sum);
    for(ii = max(i-1, 0); ii <= min(i+1, dim-1); ii++) 
	for(jj = max(j-1, 0); jj <= min(j+1, dim-1); jj++) 
	    accumulate_sum(&sum, src[RIDX(ii, jj, dim)]);

    assign_sum_to_pixel(&current_pixel, sum);
    return current_pixel;
}

首先注意到，该循环中，avg() 函数调用的函数太多，严重影响了效率。因此，第一步就是消除一些不必要的函数调用。比如，

将 initialize_pixel_sum() 函数直接变为对 sum 变量的初始化
在循环中， min 函数和 max 函数会被多次调用，但事实上因为循环变量一直在增加，只需要进行一次取值比较
accumulate_sum 函数和 assign_sum_to_pixel 函数也可以变为简单的几条语句。

经过上述改进后，取得了一定的优化效果，但我认为还不够。在不考虑图像的边界情况时，中间的图像点在计算时取出的数据有相当部分是重合的。因此，可以先从0开始，在处理完边界情况后，对于中间的像素点做同时计算处理，从而充分利用高速缓存。

// dst中间主体部分处理
for(j=1;j<dim2;j+=2)
{        
    // 同时处理两个像素
    dst->red=(P1->red+(P1+1)->red+(P1+2)->red+P2->red+(P2+1)->red+(P2+2)->red+P3->red+(P3+1)->red+(P3+2)->red)/9;
    dst->green=(P1->green+(P1+1)->green+(P1+2)->green+P2->green+(P2+1)->green+(P2+2)->green+P3->green+(P3+1)->green+(P3+2)->green)/9;
    dst->blue=(P1->blue+(P1+1)->blue+(P1+2)->blue+P2->blue+(P2+1)->blue+(P2+2)->blue+P3->blue+(P3+1)->blue+(P3+2)->blue)/9;
    dst1->red=((P1+3)->red+(P1+1)->red+(P1+2)->red+(P2+3)->red+(P2+1)->red+(P2+2)->red+(P3+3)->red+(P3+1)->red+(P3+2)->red)/9;
    dst1->green=((P1+3)->green+(P1+1)->green+(P1+2)->green+(P2+3)->green+(P2+1)->green+(P2+2)->green+(P3+3)->green+(P3+1)->green+(P3+2)->green)/9;
    dst1->blue=((P1+3)->blue+(P1+1)->blue+(P1+2)->blue+(P2+3)->blue+(P2+1)->blue+(P2+2)->blue+(P3+3)->blue+(P3+1)->blue+(P3+2)->blue)/9;
    dst+=2;
    dst1+=2;
    P1+=2;
    P2+=2;
    P3+=2;
}