深入理解计算机系统之位操作实验
深入理解计算机系统——位操作实验
实验介绍
实验资料可从CSAPP 官网获取。
本实验考察了位操作符的使用以及整数和单精度浮点数的位级表示。通过完成这 15 个有关位运算的题目,可以加深大家对计算机中数据的理解。注意,所有要实现函数都位于 bits.c 文件。
-
bits.c唯一需要修改的源代码文件 -
btest.c该文件用于评估位操作实现功能的正确性,每次实现一个函数后,建议使用btest来检查功能是否正确:1
2$ make
./btest也可以使用
-f标志检查单个函数的正确性,例如1
$ ./btest -f bitXor -
dlc 语法检查,检查是否使用了违反规定的操作。如果程序没有输出,说明我们的程序没有问题。
位运算实现
bitXor
题目要求:使用 ~ 和 & 实现 x ^ y。
关于这个函数的实现,我首先想到了在数字电路课程中学到的技巧:和式转乘积。设两个输入分别为 A 和 B,那么其亦或操作可表示为:$ A \bar{B}+\bar{A}B = \overline{\overline{A\bar{B}} \cdot \overline{\bar{A}B}}$。如此转换,等式中仅存在 ~ 和 & 运算。于是,代码可写为:
1 | |
tmin
题目要求:返回二进制补码下的最小整数。
这题非常简单,只要略知补码的表示方式就行。
1 | |
isTmax
题目要求:判断 x 是否是二进制补码下的最大数,若是返回 1。仅能使用 ! ~ & ^ | + 。
首先明确,二进制补码下最大数是 0x7fff ffff。其次明确,可以通过加法等方式,在特点条件下获得结果 0 ,然后取反,来完成对相应数字的判断。我最先想到的是,通过判断 x 加上其反码再加一是否为 0 来决定,后来发现不对,所有数都满足这一条件 :sweat_smile:。
仍采取加法策略 0x7fff ffff+1=0x8000 0000,然后再累加,得到 0 ,但这样还不够,因为 -1 也满足要求。注意到,0xffff ffff +1 = 0x0 ,于是 !!(x+1) 可以判断是否为 -1,于是:
1 | |
allOddBits
题目要求:判断 x 中的奇数位置是否全为 1,若是返回 1。比如 0xAAAA AAAA 就满足要求。
与上题同样的思路:找出某运算过程,使得符号要求的数字经计算后得到 0,从而判断命题真伪,我取名为得 0 思想 。判断 x 的某位是否为 1 ,有两种做法:一是 x 与 1 取 & ,即 & 的保持性,二是 x 与 0 取 | ,即 | 的保持性。该使用哪一种?第二种。因为第一种要求立即数奇数位为 1 才能有区分性,但偶数位得出的结果是不定的,因此使用第一种后,计算得出的结果会难以判断问题的真伪。
而第二种中,要求立即数奇数位为 0 才能有区分性,若立即数偶数位全为 1 ,那么 | 运算后,偶数位一定都是 1 ,这是确定的。

1 | |
negate
题目要求:返回 -x 的值。
这题非常简单,二进制补码中,求相反数只需取反再加一就行
1 | |
isAsciiDigit
题目要求:判断输入的 x 是否是数字的 ASCII 码。
收到前面几题的影响,我一开始仍从得 0 思想入手。但感觉 0x30 到 0x39 的二进制共同特征不太明显,故放弃。再从上一题的求 -x 出发,只要判断 x >= '0' && x <= '9' 即可。
1 | |
conditional
题目要求:实现三运算符:x ? y : z 。
关键在于,如何选定 y 和 z 。使用 & 的保持性,答案就非常简单:
1 | |
当 [0] 处为 -1,[1] 为 0 ,整个运算值就是 y ,反之为 z !当然,使用 | 的保持性也是可行的。在不使用 if 的情况下,可以使用 !x 判断 x!=0。总结一下,x!=0 时,[0] 为 -1,x==0 时,[1] 为 0。
1 | |
isLessOrEqual
题目要求:判断 x<=y 是否成立,若成立返回 1,否则返回 0。
判断大小,使用减法。在只能使用 + 的情况下,需转换为x-y = x+ ~y+1 。注意到,x-y 判断比 y-x 更复杂(还要验证 0 的情况),因此使用 y-x 。再考虑溢出的情况:当 y 为正数,x 为负数,y-x 却为负数,便发生了溢出,应当返回 1 ,却返回了 0 。当 y 为负数,x 为正数,y-x 却为正数,应当返回 0 ,却返回了 1 。
后来发现,问题可以进一步简化,先取出符号位,当 y 为正数,x 为负数时直接为真。然后再相减,更加方便。
1 | |
logicNeg
题目要求:实现 ! 运算
问题可改为,如何判断一个数全为 0 。注意到,-x 相当于按位取反再加一,如果 x 为 非 0 数,那么 x|(-x) 后必定为 -1 。利用这个性质,即可判断是否为 0 。
1 | |
howManyBits
题目要求:求出 x 最少需要多少 bits 来表示。
这题就比较难,判断最少需要多少 bits 来表示 x ,实际上就是去掉那些无用的高位 bits。对正数而言,这题等价于求最高位1出现的位置,然后把高位的 0 删到仅剩一个符号位。而对负数而言,这等价于求负数的最高位 0 出现的位置,因此需要预处理。类似于 x ? y : z 的实现,依旧使用 & 的保持性,先搭出框架:
1 | |
然后填写 [0] 和 [1],算出答案就不难了。
对于正数而言,需要找到最左边的 1。而对于负数,只要按位取反后,便可同样处理。找最左边的 1 ,可以使用二分法:
1 | |
但实验要求不能使用 if 语句,因此需要手动实现:
1 | |
floatScale2
题目要求:返回与 f*2 等价的二进制补码下的整数。
只要熟悉了浮点数的 IEEE 表示方法,这题便不难解决。
浮点数的表示方法简介如下:

-
denormalized
exp = 0,E = 1 - Bias = -126,F = 0.frac,将 frac 左移1位。这里有一种特殊情况,如果 frac 最高位为1,最高位左移后,会移动到 exp 中,此时 E = 1 - Bias 仍为 -126,而 F = 1.frac ,因此同样正确。可以说,这个指数设计得相当巧妙!
-
special
exp = 0xFF,当frac = 0时,代表无穷大,无穷大的2倍同样是无穷大,此时直接返回;当frac != 0时,代表NaN,直接返回。所以当exp = 0xFF时直接返回函数参数。
-
normalized M = exp - Bias, M = 1.frac,将exp+1
于是,不难得到:
1 | |
floatFloat2Int
题目要求:返回 (int)f 等价的二进制整数
仍然考察了浮点数 IEEE 表示。需要考虑三种情况:
- denormalized,非常接近 0 的数,转换为 int 值后为0
- normalized,数的分布从接近 0 到无穷,且越来越稀疏,当 f 不超过int型表示的范围时,转换为 int,当超过int 型表示的范围时返回
0x8000 0000 - special,返回
0x8000 0000
重点是,将 normalized float 转换为整数,F=1.frac ,M = F * 2^E
- 如果E >= 31,小数点右移31位,此时隐含的1和 frac 占32位,所以还需要一个符号位,超出了int范围
- 如果E < 0,M = 0.1frac,转换为int后为0
- 如果0 < E < 23, 小数点右移E位后,需要舍弃 F 中部分位。直接将 F 左移 23-E 位,抹去小数部分
- 如果23 <= E < 31,将 F 左移 E-23 位,并在后面补零
1 | |
floatPower2
题目要求:返回 2.0^x 相等价的二进制表示整数。
根据 IEEE 浮点数表示,有几个边界需要注意
x>127太大,返回 NaNx<-148太小,返回0x>=-126normalized float- 其余情况为 denormalized float
然后,就按照要求一步步填空,完成任务。
1 | |
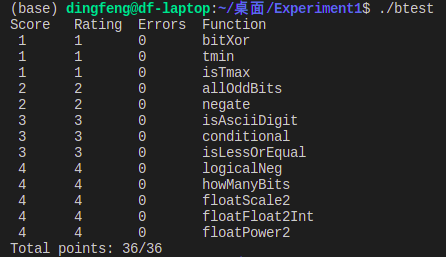
实验结果
如果所有函数都编写完成,编译运行后,出现如下结果,那么本实验就圆满完成了 :smile:。