并行程序中的求和

并行求和算法实现

题目描述

有 $N$ 个处理器，现对 $N$ 个数求和，要求每个处理器中都保持全和。有两个算法可以实现：

• 蝶式求和算法：重复计算元素的求和，共需要 $logN$ 步。在每个阶段，处理器都会将数据发给指定的其他处理器，然后进行求和。
• 二叉树求和算法，累计求和，在广播给其他节点，需要 $2logN$ 步

蝶式算法实现

首先需要假定：数据均匀地分布在每一个处理器中，特别地，每个处理器中只有一个数字。但求和必然要求所有的数据，蝶式算法就是将数据从少到多，一步一步地累加起来。编程时，可按照蝶式算法一步一步按阶段地实现。接下来，对照下图，仔细地品读一下算法，了解其中的规律，以便代码实现。

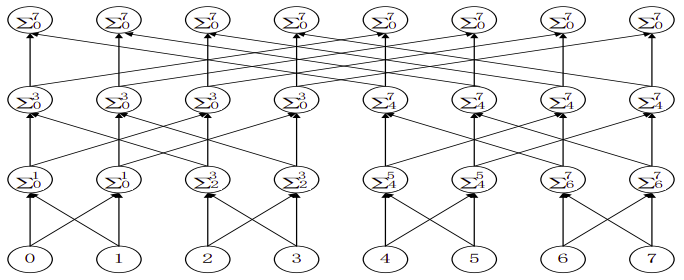
在第一阶段，每个处理器与其相邻的处理器交换它们的数据。注意一下它们的编号：Proc#0 和 Proc#1 ，Proc#2 和 Proc#3，……如果我们把这些编号全部写成二进制，规律就更加明显了😄。这些互相交流的处理器的编号，除了倒数第一位是不一致的，其他都是一致的！

第二个阶段，处理器0与2号处理器交流，1号与3号交流，4号与6号交流……在二进制表示中，也是只有一个位的差别，这里是倒数第二位。第三阶段，0号处理器与4号交流，是倒数第三位的差别。

得到规律：在第 i 个阶段，处理器 Proc#n 会与处理器 Proc#(n ^ (1 << (i-1))) 交换数据（发送和接收都要），然后相加就行了😆 。如此一来，代码就呼之欲出了。

for(int i = 2; i <= num_procs; i <<= 1) {
    int tag = i >> 1;
    int dest = id_procs ^ tag;
    MPI_Send(&data, 1, MPI_INT, dest, tag, MPI_COMM_WORLD);
    MPI_Recv(&recvdata, 1, MPI_INT, dest, tag, MPI_COMM_WORLD, &status);
    data += recvdata;
}

二叉树求和实现

二叉树求和的过程非常好理解：先将相邻的处理器数据收集起来，求和后再次重复，直到求出总和，最后沿着二叉树的路径将求和结果往下传导。

虽然二叉树求和算法的实现相较于蝶式求和更容易理解，但实现起来却相对吃力，并且还会更加耗时。因为它还要求将数据从根部传下来，多了一个要实现的阶段。

还是找规律，第一个阶段，0号处理器与1号处理器相加，Proc#2 与 Proc#3 相加，我假设求和后的数据都存放在较小编号的处理器中，那么第二阶段，就是 Proc#0 与 Proc#2 相加，第三阶段（如果有的话），就是 Proc#0 与Proc#4 相加。同样从二进制入手，找到如下规律：**在第 i 个阶段，相互之间通信的处理器中仅第 i 位不一致。**还需要注意的是，编号较小的处理器接收数据，较大的发送数据。好，现在理解计算这部分代码就没有难度了 :yum:。

for(int i = 2; i <= num_procs; i <<= 1) {
    int tag = i >> 1;
    int diff = id_procs & tag;
    if (diff) {
        MPI_Send(&data, 1, MPI_INT, id_procs-tag, tag, MPI_COMM_WORLD);
    } else {
        MPI_Recv(&recvdata, 1, MPI_INT, id_procs+tag, tag, MPI_COMM_WORLD, &status);
    }
    data += recvdata;
}

然后就是将 Proc#0 处理器中的计算结果分发给其他处理器。当然，使用 MPI_Bcast() 函数直接将数据广播出去会更加方便，但是这样做不符合算法的要求 :man_shrugging:。我们需要弄清楚两点：哪一个处理器接收？哪一个处理器发送？第一步，当然是 Proc#0 处理器发送，让 Proc#N/2 处理器接收。第二步，Proc#0 与 Proc#N/4 通信，Proc#N/2与 Proc#3N/4 通信……emm，看起来我们需要拿出纸笔，好好算一算。每次发送/接收消息，处理器编号的差都是 $i/2$，而且只有编号是 i 的倍数的处理器才能发送消息。把循环变量当做处理器总数，并每次除 2，可以方便我们对处理器编号的计算。

计算完后，在编写代码，就可以一步到位，省去了很多调试的烦恼！如果大家没看懂代码，或许上图可以帮助大家理解。

for(int i = num_procs; i >= 2; i >>= 1) {
    int tag = i;
    if (id_procs % i == 0) {
        MPI_Send(&data, 1, MPI_INT, id_procs+(i>>1), tag, MPI_COMM_WORLD);
    } else if(id_procs % (i >> 1) == 0) {
         MPI_Recv(&data, 1, MPI_INT, id_procs-(i>>1), tag, MPI_COMM_WORLD, &status);
    }
}

所有算法的代码实现请见我的 github仓库