Why RISC-V ?

Why RISC-V

读 Design of the RISC-V ISA 论文后的总结与思考。这是本系列的第三部分，在认识了 RISC-V 的基本 ISA 后，接下来我们介绍 RISC-V 的标准扩展，进一步体会这样设计带来的好处。

设计 RISC-V 时，我们定的一个目标就是使 RISC-V 能够既适用于资源紧张的低端实现，又能够适用于高性能计算实现。前者需要一个精简的 ISA ，后者要求一个高能效（意味着注定较为复杂的）ISA ，这就要求保留一些在嵌入式处理器或在任何通用处理器中非常重要的特性。RISC-V 用添加扩展的形式提供了很好的灵活性。RISC-V 目前有四种标准扩展——M 用于整数乘法和除法，A 用于原子内存操作，F 和 D 用于单精度和双精度浮点，它们一起构成了用于通用计算的强大 ISA。

整数乘除

在许多应用中，特别是那些有很多的定点计算的软件中，整数乘除法是常见的运算。虽然它们在计算操作中不占主导，但当软件运行时，就会发现它们仍可以占据很大一部分运行时间。因此，对于大多数应用程序来说，硬件加速这些操作是必须的。图中显示了 RISC-V M 的若干指令。

我们考虑将 M 扩展进一步分解为单独的乘法和除法扩展，但要明白一点，得出这两种扩展的需求的过程是紧密相关的。此外，若迭代乘法器在低端的 ASIC 上已实现，那么其实可以用较小的代价设计出迭代除法器。另一方面，对于许多 FPGA 来说，除法要比乘法困难得多，但由于乘法块的存在，处理器可以选择 trap 除法指令并在软件中模拟它们。

与其他 RISC ISAs 为乘法和除法指令添加了特殊的结构寄存器不同，RISC-V M 扩展中的指令直接在整数寄存器上操作。这一设计消除了与特殊的结构寄存器来往发数据的步骤，减少了指令条数以及延迟；减少了线程转换时的上下文大小；让编译器更好地进行代码优化。对于某些实现来说，写回部分的控制逻辑略有增加，但我们觉得这一微小的成本很容易被带来的好处抵消。对于使用寄存器重命名的实现，这一策略降低了复杂性，因为它消除一类为了提供性能而需要重命名的寄存器。

RV32M 增加了 4 条计算 32×32 位的乘法指令：MUL，它返回乘积的低 32 位；以及 MULH 、MULHU 和 MULHSU[^foot1]，它们都返回乘积的高 32 位，但分别将乘数和被乘数当作有符号、无符号和有符号无符号的混合处理（当然，低 32 位的乘积不需要考虑符号）。后三条指令对于定点计算是非常重要的，因为它们能够实现一个重要的优化：一个常数除法总是可以通过一个近似的倒数转化为乘法，再对乘积的高位部分进行修正（见下例）。

# compute unsigned division of a0 by 3 using multiplication
0:  aaaab2b7	lui  t0, 0xaaaab  # t0 = 0xaaaaaaab
4:  aab28293	addi t0, t0, -1365  #  = ~2^32 /1.5
8:  025535b3    mulhu a1, a0, t0    # a1 = ~(a0 / 1.5)
c:	0015d593    srli a1, a1, 0x1    # a1 = (a0 / 3)

[^foot1]: MULHSU 对于多字有符号乘法很有用，因为当乘数的最高有效字（包含符号位）与被乘数的较低有效字（无符号）相乘时，就需要用到它，这是多字有符号乘法的子步骤。

还有四条指令执行 32×32 位的除法：DIV 和 DIVU，它们用于有符号除法和无符号除法；还有 REM 和 REMU，用于求有符号余数和无符号余数。在 C99 之后，带符号的除法会向 0 取整，余数与被除数符号相同。除零不会导致异常（见下引用）；希望出现异常的编程语言可以在启动除法操作后在除法后加上分支指令。注意到，高度可预测的分支对性能的影响应该是很小。

The quotient of division by zero has all bits set, i.e. $2^{XLEN}−1$ for unsigned division or −1 for signed division. The remainder of division by zero equals the dividend. Signed division overflow occurs only when the most-negative integer, $−2^{XLEN}−1$ , is divided by −1. The quotient of signed division overflow is equal to the dividend, and the remainder is zero. Unsigned division overflow cannot occur.

最后，RV64M 扩展了这些指令，以操作 64 位寄存器，还添加了 5 条以 W 结尾的指令，这些指令对 32 位数据进行运算得到 32 位结果后，再符号扩展到 64 位。

多处理器同步

在 1962 年，Edsger Dijkstra 注意到一个由 Theodorus Dekker 设计的算法可以在仅使用常规的 loads 和 stores 下解决互斥锁问题。然而，Dekker 的算法在并发线程数量的扩展性上表现的很糟：在 n 个线程中获得一个共享锁需要 O(n) 个操作。因而，早期的并发单处理器和并行多处理器的架构师增加了硬件同步机制来加速互斥，比如 test-and-set，自动置位并返回旧值。

互斥是一种完全通用的同步机制，且 test-and-set 很容易实现。然而，这种策略不能很好地用于高度并行的系统，因为它不足以构造无等待的同步原语，比如非阻塞的生产者——消费者队列。几个可选原语就足够了；其中，原子的 compare-and-swap (CAS) 是最主流的。CAS 比较寄存器和与另一个寄存器中内存地址指向的值，若比较数相等，就将第三个寄存器的值写入到该内存地址中，这是一条通用的同步原语，其他同步操作可以以它为基础来完成。

考虑到并行计算的应用，我们设计的 RISC-V ，应当可被用于带有极多线程级并行度的系统。我们本打算让 RISC-V A 以只包含 CAS 的方式提供内存原子操作；的确，我们曾对这一选择深思熟虑。但是 CAS 需要三个源操作数（内存地址、比较和交换值），这意味着需要一个新的整数指令类型，必然使得处理器微体系结构设计复杂化，还需要增加附有额外数据字的内存系统命令形式。因此，我们参考了几个早期 RISC ISAs（包括 MIPS 和 Alpha ）的做法，提供了 load-reserved（LR）和 store-conditional（SC）指令。这些低级的原语将原子操作拆分为 load、compute 和 store 三个阶段。LR 执行正常的 load，但注册了一个在内存上的保留。如果时间过长，或者另一个处理器请求相同的地址，该保留会被取消。SC 尝试执行 store ，但只有在拿到保留时才会成功；此外，它将成功或失败的标志写入一个目的寄存器 rd ，以便程序可以根据结果进行分支。通常，LR/SC 序列形成循环体，循环直到 SC 成功为止。

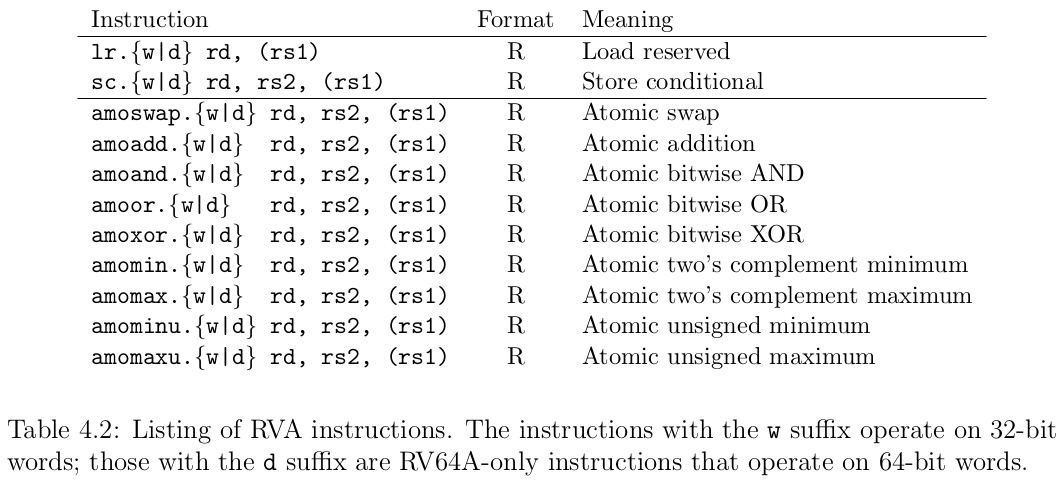
具体来说，LR 和 SC 保证了它们两条指令之间的操作的原子性。LR 读取一个内存字，存入到 rd 寄存器中，并留下这个字的保留记录。而如果 SC 的目标地址上存在保留记录，它就把字存入这个地址。如果存入成功，它向目标寄存器 rd 中写入 0；否则写入一个非 0 的错误代码。

在成功执行的 SC 之后的 LR 是对修改后的内存字的原子操作。换句话说，没有线程可以观察到在这两者之间发生的另一个内存操作。类似地，在配对 LR 操作之前，不能认为 SC 已经发生。

LR/SC 模式的主要优点是，它既易于实现，又非常通用：它可以用来构造任何单字原子操作，包括 CAS（见示例代码）。然而， LR/SC 的简单的实现会在多个处理器争用同一个数据时，遇到活锁（livelock）的麻烦。为了解决这个问题，我们要求 LR/SC 的代码序列长度必须有限制（16 条连续的静态指令），前提是它们只包含基本 ISA 指令，除了 load 、store 以及被 taken 的分支[^foot2]。这一规定允许实现通过在限定的时间内阻止缓存中指令的插入这一简单的做法来保证机器能够继续向前（不产生活锁）。当然，它也对微体系结构施加了一些限制。指令序列最终必须能放入 cache，即使它与保留的数据冲突；例如，统一指令/数据的缓存和 TLBs 至少必须是双向集关联的。

[^foot2]: 为何规定长度必须在 16 条连续的静态指令内呢？其实这个约束有几个微妙之处。不能有 taken 分支限制了动态指令数量，16 条指令的限制意味着直接映射指令缓存的大小就足够了——只要它们可以保存至少 64 个连续的字节。

retry: lr.w t0, (a0) 		## atomically {
       bne t0, a1, fail 	## if (M[a0] == a1)
       sc.w t0, a2, (a0) 	## M[a0] = a2;
       bnez t0, retry 		## }

LR/SC 相对于 CAS 的另一个好处是，它避免了所谓的 ABA 问题，即将内存位置从值 A 修改为值 B，然后再修改回值 A 的麻烦。由于 CAS 的成功执行取决于值是否相等，因此它无法检测到这种情况，从而使无等待数据结构的实现复杂化。一种常见的解决方法是提供双字 CAS 操作，其中的第二个字用作版本号。但是，这种方法使 ISA 和实现复杂化了：双字 CAS 有四个源寄存器和两个目标寄存器操作数，并修改两个内存字。幸好，LR/SC 没有遇到 ABA 问题，因为它检测任何插入的内存写入，不论最终是否保留了该值。

Atomic Memory Operations

虽然只提供 LR/SC 原语就足够了，但我们仍提供了几个原子内存操作指令（AMOs），AMO 指令执行多处理器的同步读-修改-写操作，并使用 R-type 格式进行编码。它们对一个内存字执行简单的算术和逻辑运算，并将目标寄存器设置为操作前的内存旧值。内存读写之间的过程不会被打断，内存值也不会被其它处理器修改。这些指令的功能有加法；有符号和无符号的求最小最大值；与、或、异或运算；以及交换。这些 AMOs 为高并行系统提供了一个重要的优化：当一个内存字被竞争时，AMO 可以被发送到内存字，而不是获得对包含该字的高速缓存线的独占访问。除了减少延迟、网络占用和缓存震荡外，该策略还改善了 Amdahl 法则的瓶颈。若没有 AMOs，那么由于 LR/SC 例程包含的是一般的指令序列，因此很难执行这样的优化。当然，有的架构师认为不需要浪费硬件资源来实现 AMOs ，也可以用 LR/SC 原语合成 AMOs， microcode 或者更高特权级的 software trap 都是可以的。

我们有意识地忽略了在 sub-word 上的 AMOs，因为它们在大多数情况下很少见。最常见的 sub-word AMOs 是按位逻辑操作，然而该操作很容易由 word AMOs 实现（使用一些额外的指令来隐藏地址并转移数据）。LR/SC 序列也可以实现其他的 AMOs 。下面的代码显示了如何使用 LR/SC 实现 byte 大小的操作数的原子获取和加法操作。

	andi t0, a0, 3 # Shift
	slli t0, t0, 3 # addend
	sll a1, a1, t0 # into place.
	addi t1, x0, 255 # Generate
	sll t0, t1, t0 # mask.
	andi a0, a0, ~3 # Clear address LSBs.
retry: 
	lr.w t2, (a0) # Load operand.
	add t3, a1, t2 # Perform
	xor t4, t3, t2 # addition
	and t1, t4, t0 # under
	xor t2, t1, t2 # mask.
	sc.w t2, t2, (a0) # Attempt to store result.
	bne t2, x0, retry # Retry if store fails.

[^foot3]: 所有的 RV32A 指令都有一个请求位（aq）和一个释放位（rl）。aq 被置位的原子指令保证其它线程在随后的内存访问中看到顺序的 AMO 操作；rl 被置位的原子指令保证其它线程在此之前看到顺序的原子操作。想要了解更详细的有关知识，可以查看[Adve and Gharachorloo 1996]。

RVA Memory Model

内存模型是一个非常难懂的课题，在之前的博文中，我们说过 RISC-V 采用了 relaxed memory model ，因此一个线程看到的另一个线程的内存访问可以是乱序的，除非执行一个 FENCE 指令以保证一个特定的顺序。这与顺序一致性（sequential consistency）有很大的区别。 A 扩展中的指令可以有效地实现 release consistency (RC) 内存模型。RC 是一种宽松的一致性模型，它通过区分不同风格的同步操作，为每一种操作分配不同的、较弱的排序属性，从而允许很大程度的一致性。RC 已经成为 2011 年版本的 C 和 C++ 语言的标准内存模型，并且它一直兼容 Java 内存模型。

在 RC 中，共享内存访问被分为了普通访问——乱序也不会导致竞争的 loads 和 stores，和特殊访问。RC 引入了两种重要的特殊访问：获取（acquire）和释放（release）。acquire 用于获得对共享变量的访问，而 release 操作释放了该变量的控制权。它们通常与获取互斥锁和释放互斥锁相关联。acquire 和 release 原语的语义是由 RC 模型中的内存顺序约束给出的，如图所示。在允许执行普通的加载和存储之前，必须执行所有的 acquires。同样地，在允许执行 release 之前，所有之前的普通加载和存储必须已经执行。最后，特殊访问必须是完全有序的。

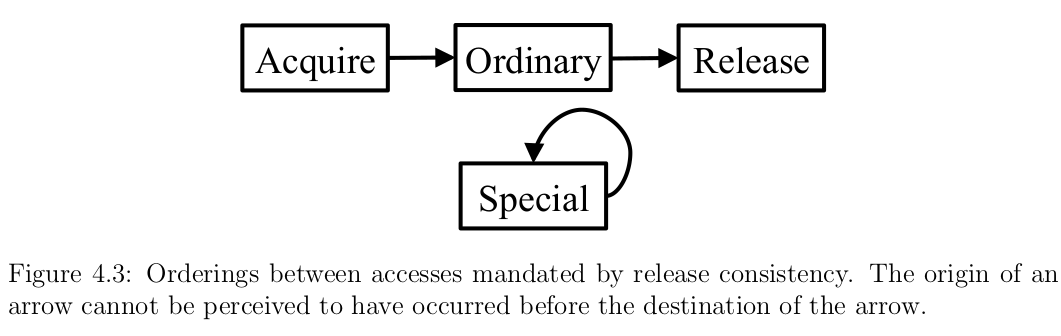
这一限制导致了更严格的 RC ，称之为 RCsc ，其特殊访问必须顺序一致性（sequential consistency）。这个关键的特性支持无数据竞争的编程模型，它是硬件和软件之间的一种契约，保证了它看上去像顺序一致的内存系统，前提是对所有特殊访问都进行了适当的注释。其结果是，对于一类重要的程序，RCsc 既提供了 relaxed model 的更大并发性，又提供了顺序一致性的更简单的编程模型。

**A** 扩展中的指令通过加上内存顺序注释来实现 RCsc 内存模型，在静态指令上的两位：aq 和 rl[^foot3] 。当 aq 位被设置在 LR 、SC 或 AMO 上时，该指令被当作 acquire 访问，在同一个线程中不会看到在该指令之前的任何内存访问。当 rl 位被设置时，指令被当作 release 访问，这样它就不会被认为是在任何内存访问之前执行的。当 aq 和 rl 都没有设定时，就没有特定的顺序保证，适于组合简化。当两者都被设置时，该访问就是相对于其他访问顺序一致。

单精度浮点运算

浮点计算在一些应用领域是普遍存在的，甚至许多面向整数的程序使用足够的浮点来证明硬件支持。然而，基本 ISA 中排除了浮点指令，以支持不会使用它们的嵌入式实现，而且浮点运算最好是由附加的协处理器处理的处理。RISC-V F 扩展增加了对单精度浮点的支持，符合 IEEE 754 浮点运算标准。

在定义 F 扩展时，最有争议的决定就是：是否要将整数寄存器用于浮点计算？还是添加专用的浮点寄存器？前一种策略将简化 ISA，降低的实现成本，并减少上下文切换时间。尽管如此，我们最终还是选择添加了一组新的浮点寄存器，如上图所示，因为我们觉得优点大于缺点：

整数寄存器和浮点寄存器的位宽不一定相同，例如，RV32 机器可能具有双精度浮点运算
我们希望实现能更灵活地使用内部编码格式，例如，在硬件中加速对非正规数（subnormal numbers）的处理时，不在同一个寄存器中表示整数和浮点数可以简化这种设计
添加一组新的寄存器文件可将寄存器容量和带宽翻倍，因为操作码（浮点数与整数肯定不同）提供了一个隐式说明，所以不需要改变指令格式，但可以提高处理器的性能
添加一组新的寄存器文件，事实上很自然地提供了一个寄存器文件的分库策略，简化了超标量对寄存器文件端口的实现
通过向寄存器文件中添加由微架构管理的脏位，可以减轻上下文切换的成本

为了支持内部编码格式，我们决定避免在浮点寄存器中表示整数。这与 SPARC 、Alpha 和 MIPS 不同，它们完全在浮点寄存器文件中进行定点的转换，RISC-V 使用整数寄存器对这些指令进行操作。这种选择缩短了混合格式下常用的指令序列——例如，在地址计算中使用整数转换的结果时。

大多浮点运算的结果会进行四舍五入，但四舍五入方案因编程语言和算法而异。RISC-V 提供了五种四舍五入模式，其编码如下表所示：四舍五入到最接近的数字，并向偶数断开；舍入为零；向-∞舍入；向+∞舍入；四舍五入到最接近的数字，向零四舍五入。(IEEE 754-2008 只需要前四个，但根据我们的经验，第五个对于手工编写库例程很有用）。

Rounding Mode	Mnemonic	Meaning
000	RNE	Round to Nearest, ties to Even
001	RTZ	Round towards Zero
010	RDN	Round Down (towards −∞)
011	RUP	Round Up (towards +∞)
100	RMM	Round to Nearest, ties to Max Magnitude
111	DYN	Dynamic rounding, based on frm register

在大多数编程语言中，四舍五入的方向应动态指定。对此，我们规定所有浮点指令都可以使用动态舍入模式，在浮点控制和状态寄存器的 frm 字段中设置，其格式为下图所示。此外，一些操作，比如在 C 和 Java 中从浮点类型强制转换为整数类型，需要在特定方向上舍入。在不修改动态舍入模式的情况下支持这些操作是可取的，而且还有助于加速库例程的实现，比如先验函数。因此，我们为所有浮点运算提供了动态舍入模式或静态选择其中一种。这个额外的 3 位字段会使 F 扩展消耗了大量的编码空间，但我们认为通用性和提升的性能证明这些开销是合理的。

异常处理

大多数浮点运算会产生 IEEE 754 标准下的异常：指示算术错误或不精确的运行时条件。一共有 5 种异常：无效运算（对 -1 开根号）；除零；上溢出；下溢出；不精确（指存在舍入）。IEEE 标准没有规定这些异常是否会导致陷阱。在 RISC-V 中，我们选择不将这些异常变为陷阱，以方便非推测性的乱序完成浮点操作。如果不这样做，顺序流水线的实现将不得不在不精确 trap 和顺序完成之间进行选择，前者暴露了实现细节并使系统软件复杂化，而后者要么使流水线变深，要么降低了性能。

虽然我们不将这些异常变为陷阱，我们仍然有可能编写对浮点异常进行处理的软件。这五个异常放入到浮点状态寄存器后，软件可以检查这些寄存器，并根据它的值转移到用户级异常处理程序。由于触发应计异常标志是一种关联操作，因此应计异常寄存器仍然允许无序指令完成。直接操作异常标志的指令只需要互锁，直到所有未完成的指令完成，再接着处理异常就可以了。

NaN 的产生与传播

IEEE 754-1985 浮点标准使几个商业竞争对手达成妥协，共同寻求结束 Velvel Kahan 所描述的那种状态——浮点算术中的“无政府状态”（当然，对于有些人来说这一不那么无私的决定是为了防止 Intel 不遵守标准😓）。为了尽量减少各派之间的不满，标准给实现留下了一些细节，例如，应该在四舍五入之前还是之后检测下溢出，NaN 是如何生成和传播的，以及如何区分 signaling NAN 和 quiet NaN[^foot4]。

[^foot4]: 分别有两者类型的 NaN，一个叫 quiet NaNs 另一个是 signaling NaNs. Quiet NaNs 被用作传播无效操作或值等错误。Signaling NaNs 可支持更加复杂的特性，比如混合数值和符号计算或者其他基本的浮点数运算扩展。

然而，标准留下的回旋的余地却导致了一个惊人的分裂。看看下面的表格，不同的 ISAs 对 NaN 的编码几乎完全不同。MIPS 和 PA-RISC 选择用 quiet bit clear来表示 quiet NaN，这违反了 IEEE 754-2008 标准。其他的区别在于其余的尾数（也叫有效位数，Significand）部分是 1 还是 0 ，以及比较惊讶的是，符号位是否设置了。至于 RISC-V NaN，我们选择将符号位清零，除 quiet bit 之外所有尾数位都清零的方案。即如果一个浮点运算的结果是 NaN，那么它就是 canonical NaN。canonical NaN 有一个正的符号位（即 0），除了 MSB （也叫做 quiet bit）之外，所有的符号都清零。在 RISC-V 中，对于单精度浮点数，canonical NaN 对应于 0x7fc00000 。这样做的原因有四：

ISA	Sign	Significand(23 bits)	QNaN Polarity[^foot5]
SPARC	0	11111111111111111111111	1
MIPS	0	01111111111111111111111	0
PA-RISC	0	01000000000000000000000	0
x86	1	10000000000000000000000	1
Alpha	1	10000000000000000000000	1
ARM	0	10000000000000000000000	1
RISC-V	0	10000000000000000000000	1

[^foot5]: QNaN polarity refers to whether the most significant bit of the significand indicates that the NaN is quiet when set, or quiet when clear.

与至少一个其他 ISA (ARM) 相同的缺省 NaN，这样做不会加剧 IEEE 754 的分化
与 Java 编程语言的 canonical NaN 相同（大多数其他编程语言都没有定义）
根据 IEEE 754 标准以及 RISC-V 的 QNaN polarity ，quiet NaN 事实上有 $2^{22}$ 个，而signaling NaN 有 $2^{22}-1$ 个（因为尾数全 0 对应的是无穷大）。而恰巧 canonical NaN 是唯一的一个不能从 signaling NaN 转为 quiet NaN 的 quiet NaN 。因此，对于可传播 NaN 的系统而言，刚生成的 NaN 可以与传播的 signaling NaN 相区别
清除 MSB 比设置 MSB 硬件成本更低。一些功能单元已经需要一个数据路径来提供尾数中的 0，但没有相应的数据路径来提供所有的 1

IEEE 754 标准还提供了将 NaN 有效负载（即非 MSB 的尾数位）从 NaN 产生开始传播到输出操作的选项。该特性旨在保存诊断信息，例如 NaN 的起源。但出于三个原因，RISC-V 不提供这个特性：

NaN 有效负载太小，无法保存完整的内存地址，因此很难使用该特性对有意义的诊断信息进行编码
因为在标准中 NaN 有效负载传播是可选的，所以可移植软件大都不依赖该特性，因此该特性很少被使用
传播 NaN 有效负载会增加硬件成本

相对于的，当一条计算指令发出 NaN 时，我们要求它是 canonical NaN 即可。当然，实现可以自由地将 NaN 有效负载传播方案作为非标准的扩展提供，由非标准处理器模式位启用，不过我们的默认方案仍然是强制性的。

浮点指令

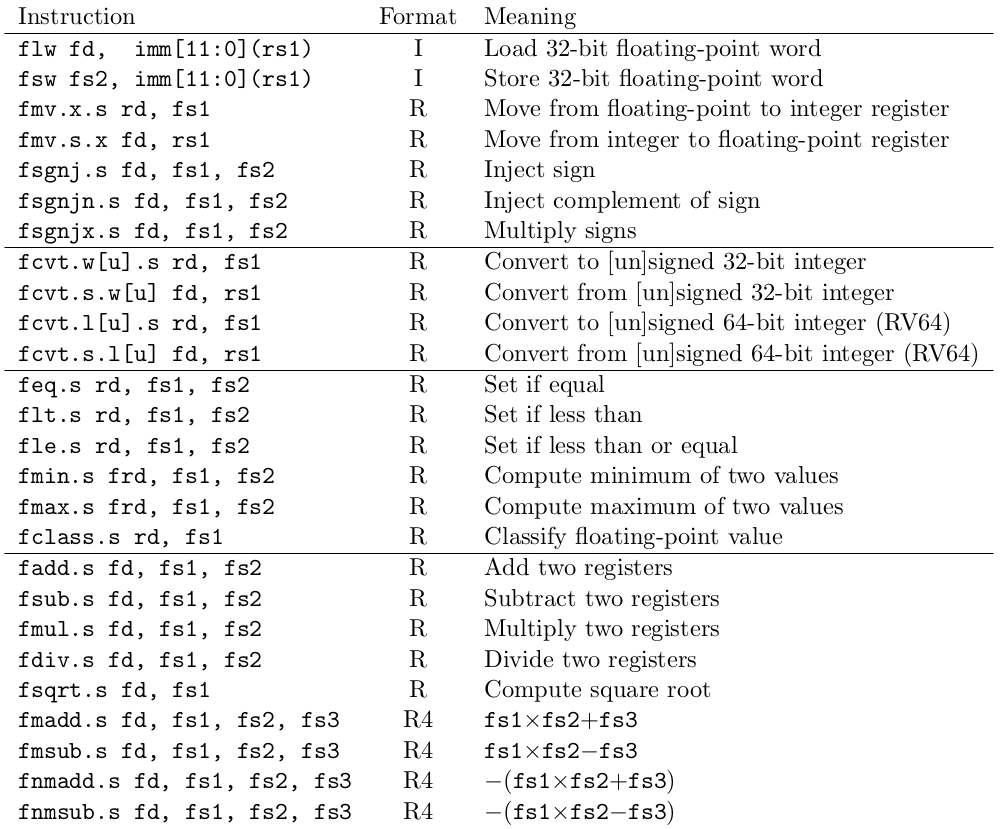
上图列出了 30 条 RISC-V F 扩展的新指令。它们分为四类：数据移动指令，转换指令，比较指令和算术指令。数据移动指令中，有新的 loads 和 stores 指令，FLW 和 FSW ，它们负责数据在内存和浮点寄存器之间移动，还包括了数据在浮点寄存器和整数寄存器之间移动的指令，FMV.X.S 和 FMV.S.X 。有些 ISAs 比如 SPARC 和最初的 Alpha ，省去了这些指令，用一个临时内存来代替实现这一功能。这种设计消除了流水线冒险，但却大大增加混合格式代码长度。下面的代码块就证明了这点。没有 FMV.X 等指令，就要多 60% 的指令，并可能会导致数据缓存未命中，降低性能。

fmv.x.s a0, fa0 					addi sp, sp, -16
srli a0, a0, 23 					fsw fa0, 0(sp)
andi a0, a0, 0xff 				lw a0, 0(sp)
addi a0, a0, -127 				srli a0, a0, 23
jalr x0, ra, 0 					andi a0, a0, 0xff
								addi a0, a0, -127
								addi sp, sp, 16
								jalr x0, ra, 0

;WITH FMV.X.S 					WITHOUT FMV.X.S

F 指令的一个新特点是符号注入指令（sign-injection instruction）。FSGNJ 、FSGNJN 和 FSGNJX 指令。它们会得到一个从 rs1 中取出的除符号位之外所有位的结果。对于 FSGNJ，结果的符号位为 rs2 的符号位；对于 FSGNJN，结果的符号位与 rs2 的符号位相反；FSGNJX 的符号位是 rs1 和 rs2 寄存器符号位的异或值。当两个源操作数相同时，这些指令可用于移动、取反或取绝对值。更通常的情况下，它们对于手工编写的浮点库例程很有用。

转换指令负责完成整数与浮点数的转换。凡是要用到整数的地方都用整数寄存器，这可以提高混合形式代码的性能，因为这显式地减少了两组寄存器之间的移动。不在浮点寄存器中表示整数可以简化内部重编码浮点格式的实现。四条转换指令有：转换到有符号整数（FCVT.W.S 和 FCVT.S.W）和无符号整数（FCVT.WU.S 和 FCVT.S.WU），并支持任何舍入模式。

比较指令会得到一个相等或不等测试的布尔结果，并将布尔值写入 rd 寄存器。FEQ.S 比较了两个浮点数是否相等；FLT.S 比较 rs1 是否小于 rs2 ；FLE.S 比较 rs1 是否小于等于 rs2 ；当其中一个源操作数为 NaN 时，结果总是 false 。FLT 和 FLE 在 quiet NaN 下会抛出了一个无效的异常，就像 C 中 < 和 <= ；FEQ 则没有，和 C 中 == 一样。若要在浮点比较的结果上进行分支，则需要 BEQ 或 BNE。

另外两个比较指令是 FMIN.S 和 FMAX.S，分别计算两个浮点数的最小值和最大值。他们实现 IEEE 754 中规定的 minNum 和 maxNum，且不传播 NaN：若一个输入是 NaN，则返回另一个输入。 FMIN 的行为与 C 库的 fminf 相同。不过，它不符合常见的（a < b ? a : b），因为如果 a 或 b 是 NaN ，它的值总是 a。

最后介绍的浮点数比较指令是浮点分类指令，FCLASS.S 查看浮点数寄存器 rs1 的值，然后向整数寄存器 rd 写一个 10-bit 的掩码，用以区分该浮点数的类别。下表列出了对应位与相应类之间的关系。注意，掩码都是独热码（one-hot encode），所以使用一条 ANDI 指令就可以检测出多个类别

rd bit	Meaning
0	`rs1` is -∞
1	`rs1` is a negative normal number
2	`rs1` is a negative subnormal number
3	`rs1` is −0
4	`rs1` is +0
5	`rs1` is a positive subnormal number
6	`rs1` is a positive normal number.
7	`rs1` is +∞.
8	`rs1` is a signaling NaN.
9	`rs1` is a quiet NaN

FCLASS 指令对于手工编写的库例程很有用，因为它们通常会在不寻常的输入上进行分支，比如 NaNs。而若不适用 FCLASS ，则将数字移动到整数寄存器中，并解析其组成字段的办法需要更多的指令。

运算指令包含：加法、减法、乘法、除法、开根运算。为了合理高效地支持 IEEE 754-2008 ，RISC-V F 还提供了 4 条混合乘加的指令 FMA，用于计算 ±a×b±c 四种操作中的任何一种，且不需要中间的乘积舍入。这个性质可以加快一些浮点库例程的实现，并且通常可以提高许多算法的性能和准确性。对于一些浮点加法和乘法出现次数特定的程序，与仅使用乘法和加法的体系结构相比，使用 FMA 指令能大大减少实现高吞吐量所必需的工作。例如，考虑存储在内存中的 4×4 矩阵的密集线性代数运算 C += A×B 。若没有 FMA，这个操作需要 192 条指令，包括 272 个浮点寄存器读和 176 个写。使用 FMA ，它需要 128 条指令，包括 208 个读和 112 个写——指令数量减少了 33%，操作数量减少了 29% 。

双精度浮点运算

大多数通用系统都需要单精度和双精度浮点数，主要是因为单精度对于某些算法来说不够精确，还因为现代编程语言对双精度运算有偏见。然而，我们认为最好还是将 RISC-V F 与 RISC-V D 分开，因为在有些嵌入式领域，单精度浮点数就足够了，双精度就太昂贵了。主流的 ARM Cortex-M4 ，一个 32 位的微控制器，以及无数的数字信号处理器都体现了这点。

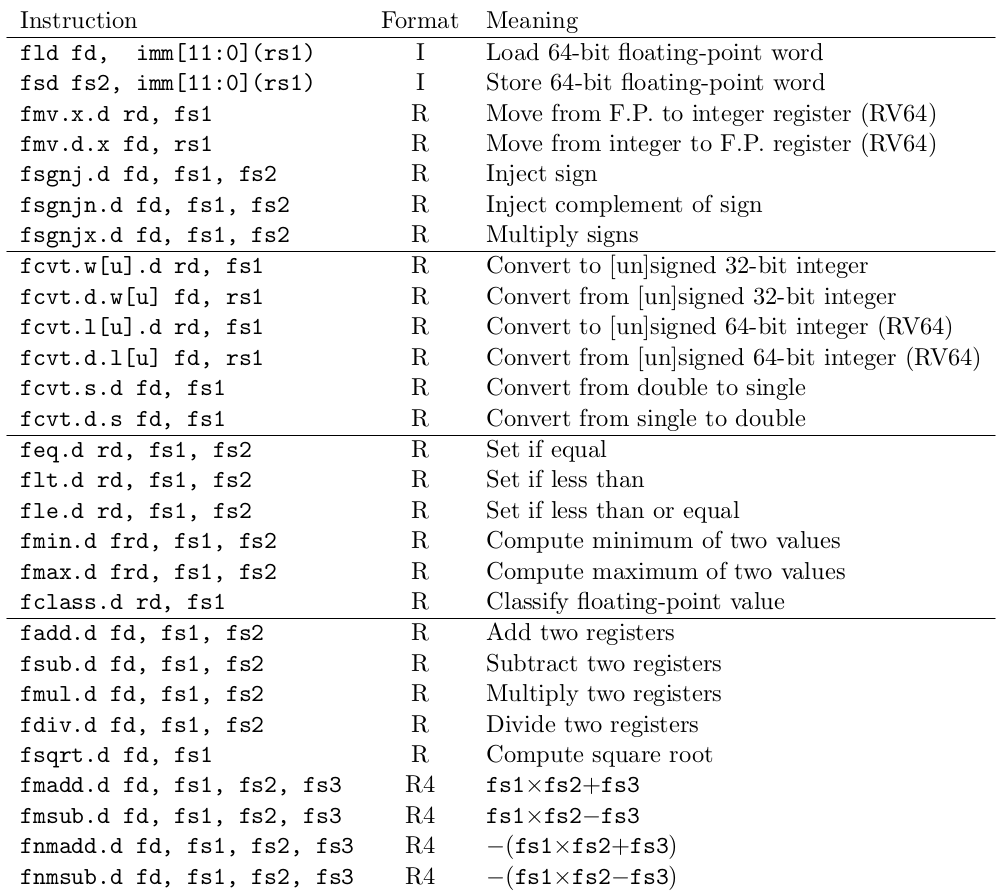
D 扩展的结构与 F 扩展非常相似，当然 F 扩展也有存在的必要。浮点寄存器的位宽变为了 64 位，且增加了对双精度数值进行操作的新指令。32 位和 64 位浮点数不能在计算指令中自由混合，但是在格式之间转换的指令（FCVT.D.S 和 FCVT.S.D），可以支持混合格式代码。

我们曾设想了另一种设计：寄存器仍为 32 位宽，双精度值对齐地存储在寄存器对中，就像在 SPARC 和 MIPS 一样。然而，这种设计不太适合寄存器重命名的实现，因为寄存器重命名会导致值的两半可能在物理上不再相邻。更重要的是，这种设计将使可用于双精度程序的寄存器数量减半，会导致寄存器阻塞，并增加指令数量。扩大寄存器的位宽似乎是最好的选择，尽管会带来额外的硬件资源消耗。

需要注意的是，在 RV32 中没有将双精度浮点数与整数寄存器文件来回移动的东西。事实上，我们曾考虑增加三条指令：FMVHI.X.D 和 FMVLO.X.D 分别用于拷贝高位/低位的浮点数值到整数寄存器，而 FMV.D.X 用于将两个整数寄存器中的数值转换为一个双精度浮点数，并将浮点数存入浮点寄存器。但是 FMV.D.X 是唯一具有两个整数源的浮点指令，所以我们认为最好完全放弃对这些操作的支持，而改用临时内存。但 RV32D 仍然支持更常见的整数数据类型转换。